10.7 线性回归模型的曲线化-多项式回归
在前面的小节中，我们假定了单一解释变量与响应变量的线性关系。对于不符合线性假设的问题，一种常用的解释方法就是通过加入多项式项来使用多项式回归模型：
其中，d为多项式的次数。虽然我们可以使用多项式回归对非线性关系建模，但由于线性回归系数w的缘故，多项式回归仍旧被看作是多元线性回归模型。
我们现在来讨论一下，如何使用scikit-lern中的PolynominalFeatures转换类在只含一个解释变量的简单回归问题中加入二次项（d＝2），并且将多项式回归与线性回归进行线性拟合比较。步骤如下：
1）增加一个二次多项式项：
2）拟合一个用于对比的简单线性回归模型：
3）使用经过转换后的特征针对多项式回归拟合一个多元线性回归模型：
从结果图像中可以看出，与线性拟合相比，多项式拟合可以更好地捕获到解释变量与响应变量之间的关系。
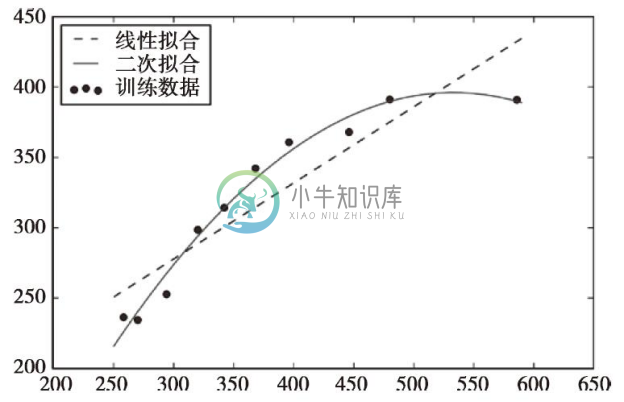
执行上述代码后，MSE的值由线性拟合的570下降到了二次拟合的61。同时，与线性拟合的结果（R2＝0.832）相比，二次模型的判定系数的结果（R2＝0.982）更好，说明二次拟合在此问题上的效果更佳。
10.7.1 房屋数据集中的非线性关系建模
在上一小节中，我们通过一个简单问题，讨论了如何通过多项式特征来拟合非线性关系。现在来看一个更加具体的例子，并将这些概念应用到房屋数据集中。通过执行下面的代码，我们将使用二次和三次多项式对房屋价格和LSTAT（弱势群体人口所占比例）之间的关系进行建模，并与线性拟合进行对比。
代码如下：
由结果图像可知，相较于线性拟合和二次拟合，三次拟合更好地捕获了房屋价格与LSTAT之间的关系。不过，我们应该意识到，加入越来越多的多项式特征会增加模型的复杂度，从而更易导致过拟合。由此，在实际应用中，建议在单独的测试数据集上评价模型的性能，进而对其泛化性能进行评估：
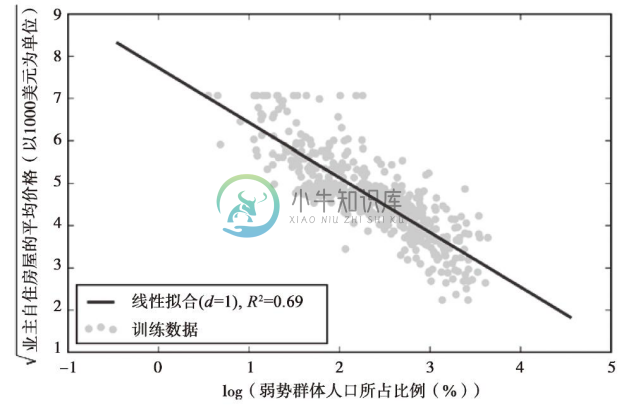
此外，多项式特征并非总是非线性关系建模的最佳选择。例如，仅就MEDV-LSTAT的散点图来说，我们可将LSTAT特征变量的对数值以及MEDV的平方根映射到一个线性特征空间，并使用线性回归进行拟合。可通过执行下面的代码对此假设进行验证：
在将解释变量映射到对数空间以及取目标变量的平方根后，我们可以捕获到两者之间的线性关系，其拟合度R2＝0.69看似优于前面使用的任何一种多项式回归：
10.7.2 使用随机森林处理非线性关系
在本节，我们将了解一下随机森林（random forest）回归，它从概念上异于本章中介绍的其他回归模型。随机森林是多棵决策树（decision tree）的集合，与先前介绍的线性回归和多项式回归不同，它可以被理解为分段线性函数的集成。换句话说，通过决策树算法，我们把输入空间细分为更小的区域以更好地管理。
1.决策树回归
决策树算法的一个优点在于：如果我们处理的是非线性数据，无需对其进行特征转换。在第3章中曾经介绍过，我们迭代地对节点进行划分来构建决策树，直到所有叶子节点的不纯度为0，或者满足终止条件时才停止迭代。当使用决策树进行分类时，定义熵作为不纯度的衡量标准，旨在通过最大信息增益（Information Gain，IG）对特征进行划分，由此可定义如下二分规则：
其中，x为待划分特征，Np为父节点中样本数量，I为不纯度函数，Dp为父节点中训练样本的子集，（D）和（D）为划分后所有节点中样本的数量。请记住，我们的目标是通过特征的划分来使得信息增益最大化，换句话说，我们试图找到使得子节点中信息不纯度最低的特征划分。在第3章中，我们使用熵作为不纯度度量，这是用于分类的一个有效标准。为了将决策树用于回归，我们使用MSE替代熵作为节点t的不纯度度量标准：
其中，Nt为节点t中训练样本的数量，Dt为节点t中训练样本的子集，y（i）为真实的目标值，
为预测目标值（样本均值）：
MSE用于决策树回归时，也常称为节点内方差，这就是分裂标准常称为方差缩减（variance reduction）的原因。为了知道决策树的拟合效果，我们使用scikit-learn中的DecisionTreeRegressor类对MEDV和LSTAT两个变量之间的非线性关系进行建模：
从结果图中可以看到，决策树捕捉到了数据的整体趋势。不过，此模型的一个局限在于：它无法捕获期望预测的连续性与可导性。此外，我们还需注意要为树选择合适的深度，以免造成过拟合或者欠拟合，在此例中，深度为3的树看起来是比较合适的：
下一节，我们将学习一种更鲁棒的决策树拟合方法：随机森林。
2.随机森林回归
正如我们在第3章中讨论的那样，随机森林算法是组合多棵决策树的一种集成技术。由于随机性有助于降低模型的方差，与单棵决策树相比，随机森林通常具有更好的泛化性能。随机森林的另一个优势在于：它对数据集中的异常值不敏感，且无需过多的参数调优。随机森林中唯一需要我们通过实验来获得的参数就是待集成决策树的数量。随机森林用于回归的基本方法与我们在第3章中讨论过的随机森林用于分类的方法基本一致。唯一区别在于：随机森林回归使用MSE作为单棵决策树生成的标准，同时所有决策树预测值的平均数作为预测目标变量的值。
现在，我们使用房屋数据集中的所有特征来拟合一个随机森林回归模型，其中60%的样本用于模型的训练，剩余的40%用来对模型进行评估，代码如下：
遗憾的是，我们发现随机森林对于训练数据有些过拟合。不过，它仍旧能够较好地解释目标变量与解释变量之间的关系（在测试数据集上，R2＝0.871）。
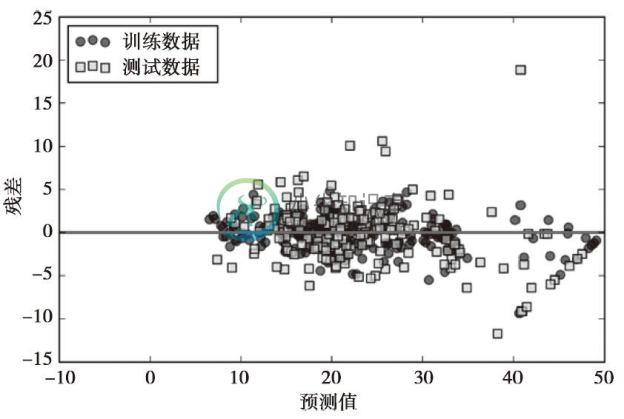
最后，让我们来看一下预测的残差：
根据决定系数R2的值可知，模型在训练数据上的拟合效果要好于测试数据，这与下图中y轴方向出现异常值所反应的情况一致。此外，残差没有完全随机分布在中心点附近，这意味着模型无法捕获所有的解释信息。不过，与本章前面小节中绘制的线性模型的残差图相比，随机森林回归的残差图有了很大的改进：
在第3章中，我们已经讨论过核技巧，并将其应用到了支持向量机（SVM）的分类中，若需要处理非线性问题，此技巧是非常有用的。虽然此话题已经超出了本书的范围，但是支持向量机的确可以用于非线性回归任务。关于支持向量机在回归中的应用问题，S.R.Gunn在其报告中做了精彩的论述：S.R.Gunn et al.Vector Machines for Classification and Regression.（ISIS technical report,14,1998），感兴趣的读者可以通过此文献了解更多信息。scikit-learn中已经实现了支持向量机的回归模型，关于其详细信息请见链接：http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html#sklearn.svm.SVR。