6.5 了解不同的性能评价指标
在前面章节中，我们使用模型准确性对模型进行了评估，这是通常情况下有效量化模型性能的一个指标。不过还有其他几个性能指标可以用来衡量模型的相关性能，比如准确率（precision）、召回率（recall）以及F1分数（F1-score）。
6.5.1 读取混淆矩阵
在我们详细讨论不同评分标准之前，先绘制一个所谓的混淆矩阵（confusion matrix）：即展示学习算法性能的一种矩阵。混淆矩阵是一个简单的方阵，用于展示一个分类器预测结果——真正（true positive）、真负（false negative）、假正（false positive）及假负（false negative）——的数量，如下图所示：
虽然这指标的数据可以通过人工比较真实类标与预测类标来获得，不过scikit-learn提供了一个方便使用的confusion_matrix函数，其使用方法如下：
在执行上述代码后，返回的数组提供了分类器在测试数据集上生成的不同错误信息，我们可以使用matplotlib中的matshow函数将它们表示为上图所示的混淆矩阵形式：
下图所示的混淆矩阵使得预测结果更易于解释：
在本例中，假定类别1（恶性）为正类，模型正确地预测了71个属于类别0的样本（真负），以及40个属于类别1的样本（真正）。不过，我们的模型也错误地将两个属于类别0的样本划分到了类别1（假负），另外还将一个恶性肿瘤误判为良性的（假正）。在下一节中，我们将使用这些信息计算不同的误差度量。
6.5.2 优化分类模型的准确率和召回率
预测误差（error，ERR）和准确率（accuracy，ACC）都提供了误分类样本数量的相关信息。误差可以理解为预测错误样本的数量与所有被预测样本数量的比值，而准确率计算方法则是正确预测样本的数量与所有被预测样本数量的比值：
预测准确率也可以通过误差直接计算：
对于类别数量不均衡的分类问题来说，真正率（TPR）与假正率（FPR）是非常有用的性能指标：
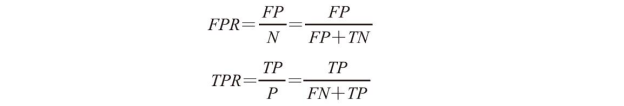
以肿瘤诊断为例，我们更为关注的是正确检测出恶性肿瘤，使得病人得到恰当治疗。然而，降低良性肿瘤（假正）错误地划分为恶性肿瘤事例的数量固然重要，但对患者来说影响并不大。与FPR相反，真正率提供了有关正确识别出来的恶性肿瘤样本（或相关样本）的有用信息。
准确率（precision，PRE）和召回率（recall，REC）是与真正率、真负率相关的性能评价指标，实际上，召回率与真正率含义相同：
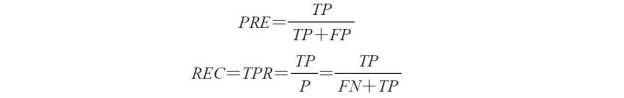
在实践中，常采用准确率与召回率的组合，称为F1分数：
所有这些评分指标均以在scikit-learn中实现，可以从sklearn.metric模块中导入使用，示例代码如下：
此外，通过评分参数，我们还可以在GridSerch中使用包括准确率在内的其他多种不同评分标准。可通过网址http://scikit-learn.org/stable/modules/model_evaluation.html了解评分参数可使用的所有不同值的列表。
请记住scikit-learn中将正类类标标识为1。如果我们想指定一个不同的正类类标，可通过make_scorer函数来构建我们自己的评分，那样我们就可以将其以参数的形式提供给GridSearchCV：
6.5.3 绘制ROC曲线
受试者工作特征曲线（receiver operator characteristic，ROC）是基于模型假正率和真正率等性能指标进行分类模型选择的有用工具，假正率和真正率可以通过移动分类器的分类阈值来计算。ROC的对角线可以理解为随机猜测，如果分类器性能曲线在对角线以下，那么其性能就比随机猜测还差。对于完美的分类器来说，其真正率为1，假正率为0，这时的ROC曲线即为横轴0与纵轴1组成的折线。基于ROC曲线，我们就可以计算所谓的ROC线下区域（area under the curve，AUC），用来刻画分类模型的性能。
与ROC曲线类似，我们也可以计算不同概率阈值下一个分类器的准确率-召回率曲线。绘制此准确率-召回率曲线的方法也在scikit-learn中得以实现，其文档请参阅链接：http://scikit-learn.org/stable/modules/generated/sklearn.metrics.precision_recall_curve.html。
在下面的代码中，我们只使用了威斯康星乳腺癌数据集中的两个特征来判定肿瘤是良性还是恶性，并绘制了相应的ROC曲线。虽然再次使用了前面定义的逻辑斯谛回归流水线，但是为了使ROC曲线视觉上更加生动，我们对分类器的设置比过去更具有挑战性。出于相同的考虑，我们还将StratifiedKFold验证器中的分块数量减少为3。代码如下：
前面的示例代码使用了scikit-learns中我们已经熟悉的StratifiedKFold类，并且在pipe_lr流水线的每次迭代中都使用了sklearn.metrics模块中的roc_curve函数，以计算Logistic-Regresssion分类器的ROC性能。此外，我们通过SciPy中的interp函数利用三个块数据对ROC曲线的內插均值进行了计算，并使用auc函数计算了低于ROC曲线区域的面积。最终的ROC曲线表明不同的块之间存在一定的方差，且平均ROC AUC（0.75）位于最理想情况（1.0）与随机猜测（0.5）之间。
如果我们仅对ROC AUC的得分感兴趣，也可以直接从sklearn.metircs子模块中导入roc_auc_score函数。分类器在只有两个特征的训练集上完成拟合后，使用如下代码计算分类器在单独测试集上的ROC AUC得分：
通过ROC AUC得到的分类器性能可以让我们进一步洞悉分类器在类别不均衡样本集合上的性能。然而，既然准确率评分可以解释为ROC曲线上某个单点处的值，A.P.Bradley认为ROC AUC与准确率矩阵之间是相互一致的[1]。
[1] A.P.Bradley.The Use of the Area Under the ROC Curve in the Evaluation of Machine Learning Algorithms.Pattern recognition，30(7): 1145-1159，1997.
6.5.4 多类别分类的评价标准
本节中讨论的评分标准都是基于二类别分类系统的。不过，scikit-learn实现了macro（宏）及micro（微）均值方法，旨在通过一对多（One vs All，OvA）的方式将评分标准扩展到了多类别分类问题。微均值是通过系统的真正、真负、假正，以及假负来计算的。例如，k类分类系统的准确率评分的微均值可按如下公式进行计算：
宏均值仅计算不同系统的平均分值：
当我们等同看待每个实例或每次预测时，微均值是有用的，而宏均值则是我们等同看待各个类别，将其用于评估分类器针对最频繁类标（即样本数量最多的类）的整体性能。
如果我们使用别二类别分类性能指标来衡量scikit-learn中的多类别分类模型，会默认使用一个归一化项或者是宏均值的一个加权变种。计算加权宏均值时，各类别以类内实例的数量作为评分的权值。当数据中类中样本分布不均衡时，也就是类标数量不一致时，采用加权宏均值比较有效。
由于加权宏均值是scikit-learn中多类别问题的默认值，我们可以通过sklearn.metrics模块导入其他不同的评分函数，如precision_score或make_scorer函数等，并利用函数内置的avarage参数定义平均方法：
