2.2 使用Python实现感知器学习算法
在上一节中，我们已经学习了罗森布拉特感知器的工作方式，现在使用Python来实现它，并且将其应用于第1章中提到的鸢尾花数据集中。通过使用面向对象编程的方式在一个Python类中定义感知器的接口，使得我们可以初始化新的感知器对象，并使用类中定义的fit方法从数据中进行学习，使用predict方法进行预测。按照Python开发的惯例，对于那些并非在初始化对象时创建但是又被对象中其他方法调用的属性，可以在后面添加一个下划线，例如：self.w_。
若读者不熟悉Python的科学计算库，或者想对其有更深入的了解，请参见如下资源：
NumPy：http://wiki.scipy.org/Tentative_NumPy_Tutorial。
pandas：http://pandas.pydata.org/pandas-docs/stable/tutorials.html。
matplotlib：http://matplotlib.org/ussers/beginner.html。
此外，为了更好地学习书中的代码，建议读者通过Packt的网站下载与本书相关的IPython notebook文件。关于IPython notebook的使用介绍，请参见链接：https://ipython.org/ipython-doc/3/notebook/index.html。
在感知器实现过程中，我们实例化一个Perceptron对象时，给出了一个学习速率eta和在训练数据集上进行迭代的次数n_iter。通过fit方法，我们将self.w_中的权值初始化为一个零向量Rm＋1，其中m是数据集中维度（特征）的数量，我们在此基础上增加一个0权重列（也就是阈值）。
与Python的列表类似，NumPy也使用方括号（［］）对一维数组进行索引。对二维数组来说，第1个索引值对应数组的行，第2个索引值对应数组的列。例如，X[2,3]表示二维数组X中第3行第4列所对应的元素。
初始化权重后，fit方法循环迭代数据集中的所有样本，并根据前面章节讨论过的感知器学习规则来更新权重。我们使用predict方法来计算类标，这个方法在fit方法中也被调用，用于计算权重更新时的类标，在完成模型训练后，predict方法也用于预测未知数据的类标。此外，在每次迭代的过程中，我们收集每轮迭代中错误分类样本的数量，并将其存放于列表self.erros_中，以便后续对感知器在训练中表现的好坏做出判定。另外，在net_input方法中使用的np.dot方法用于计算向量的点积wTx。
除了使用NumPy的a.dot（b）或np.dot（a,b）计算两个数组a和b的点积之外，还可以通过类似sum（i*j for i,j in zip（a,b））这样的经典Python for循环结构来计算。与使用Python的循环结构相比，NumPy的优势在于其算术运算的向量化。向量化意味着一个算术运算操作会自动应用到数组中的所有元素上。通过在指令序列中配置所需的算术运算，我们便可充分利用现代处理器单指令流多数据流（Single Instruction,Multiple Data,SIMD）架构的支持快速完成运算，而不是循环地对每个元素逐一进行计算。此外，NumPy还使用了高度优化的线性代数库，如使用C或者Fortran实现的基本线性代数子程序（Basic Linear Algebra Subprogram，BLAS）和线性代数包（Linear Algebra Package，LAPACK）。最后，NumPy还允许我们使用基本的线性代数操作这类加紧凑和直观的方式编写代码，如向量和矩阵的点积。
基于鸢尾花数据集训练感知器模型
为了测试前面实现的感知器算法，我们从鸢尾花数据集中挑选了山鸢尾（Setosa）和变色鸢尾（Versicolor）两种花的信息作为测试数据。虽然感知器并不将数据样本特征的数量限定为两个，但出于可视化方面的原因，我们只考虑数据集中萼片长度（sepal length）和花瓣长度（petal-length）这两个特征。同时，选择山鸢尾和变色鸢尾也是出于实践需要的考虑。不过，感知器算法可以扩展到多类别的分类器应用中，比如通过一对多（One-vs.-all）技术。
一对多（One-vs.-All，OvA），有时也称为一对其他（One-vs.-Rest，OvR），是一种将二值分类器扩充到多类别分类任务上的一种技术。我们可以使用QvA针对每个类别训练一个分类器，其中分类器所对应类别的样本为正类别，其他所有类别的样本为负类别。当应用与新数据样本识别时，我们可以借助于分类器φ（z），其中m为类标数量，并将相关度最高的类标赋给待识别样本。对于感知器来说，就是最大净输入值绝对值对应的类标。
首先，我们使用pandas库直接从UCI机器学习库中将鸢尾花数据集转换为DataFrame对象并加载到内存中，并使用tail方法显示数据的最后5行以确保数据正确加载。
接下来，我们从中提取前100个类标，其中分别包含50个山鸢尾类标和50个变色鸢尾类标，并将这些类标用两个整数值来替代：1代表变色鸢尾，-1代表山鸢尾，同时把pandas DataFrame产生的对应的整数类标赋给NumPy的向量y。类似地，我们提取这100个训练样本的第一个特征列（萼片长度）和第三个特征列（花瓣长度），并赋值给属性矩阵X，这样我们就可以用二维散点图对这些数据进行可视化了。
上述代码的执行结果如下图所示：
现在，我们可以利用抽取出的鸢尾花数据子集来训练感知器了。同时，我们还将绘制每次迭代的错误分类数量的折线图，以检验算法是否收敛并找到可以分开两种类型鸢尾花的决策边界。
执行上述代码，我们可以看到每次迭代对应的错误分类数量，如下图所示：
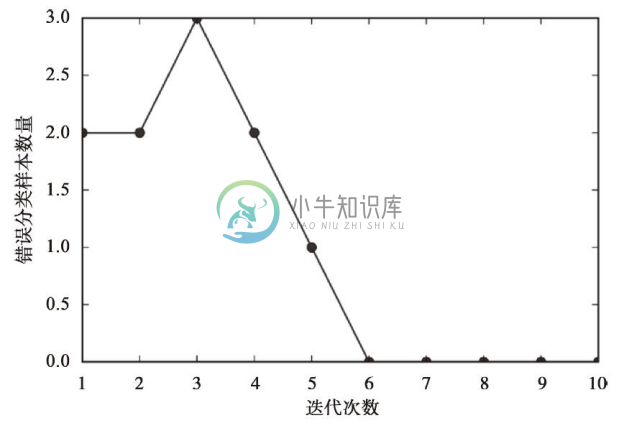
如上图所示，我们的分类器在第6次迭代后就已经收敛，并且具备对训练样本进行正确分类的能力。下面通过一个简单的函数来实现对二维数据集决策边界的可视化。
我们先通过ListedColormap方法定义一些颜色（color）和标记符号（marker），并通过颜色列表生成了颜色示例图。然后对两个特征的最大值、最小值做了限定，使用NumPy的meshgrid函数将最大值、最小值向量生成二维数组xx1和xx2。由于使用了两个特征来训练感知器，因此需要将二维组展开，创建一个与鸢尾花数据训练数据集中列数相同的矩阵，以预测多维数组中所有对应点的类标z。将z变换为与xx1和xx2相同的维度后，我们就可以使用matplotlib中的contourf函数，对于网格数组中每个预测的类以不同的颜色绘制出预测得到的决策区域。
执行上述代码，我们可以得到决策区域的图像，如下图所示：
正如我们从图中看到的那样，通过感知器学习得到的分类曲面可以完美地对训练子集中的所有样本进行分类。
虽然在上例中感知器可以完美地划分两个类别的花，但感知器所面临的最大问题是算法的收敛。Frank Rosenblatt从数学上证明了：如果两个类别可以通过线性超平面进行划分，则感知器算法一定会收敛。但是，如果两个类别无法通过线性判定边界完全正确地划分，则权重会不断更新。为防止发生此类事件，通常事先设置权重更新的最大迭代次数。