3.3 逻辑斯谛回归中的类别概率
感知器是机器学习分类算法中优雅易用的一个入门级算法，不过其最大的缺点在于：在样本不是完全线性可分的情况下，它永远不会收敛。上一小节中关于分类的任务就是这样的一个例子。直观上，可以把原因归咎于：在每次迭代过程中，总是存在至少一个分类错误的样本，从而导致了权重持续更新。当然，你也可以改变学习速率并增加迭代次数，不过感知器在此类数据集上仍旧永远无法收敛。为了提高分类的效率，我们学习另外一种针对线性二类别分类问题的简单但更高效的算法：逻辑斯谛回归（logistic regression）。请注意：不要被其名字所迷惑，逻辑斯谛回归是一个分类模型，而不是回归模型。
3.3.1 初识逻辑斯谛回归与条件概率
逻辑斯谛回归是针对线性可分问题的一种易于实现且性能优异的分类模型。它是业界应用最为广泛的分类模型之一。与感知器及Adaline类似，逻辑斯谛回归模型也是适用于二类别分类问题的线性模型，通过一对多（OvR）技术可以扩展到多类别分类。
在介绍逻辑斯谛回归作为一种概率模型所具有的特性之前，我们先介绍一下几率比（odd ratio）[1]，它指的是特定事件发生的几率。用数学公式表示为
，其中p为正事件发生的概率。此处，正事件并不意味着好的事件，而是指我们所要预测的事件，以一个患者患有某种疾病的概率为例，我们可以将正事件的类标标记为y＝1。更进一步，我们可以定义logit函数，它是几率比的对数函数（log-odds，对数几率）。
logit函数的输入值范围介于区间[0,1]，它能将输入转换到整个实数范围内，由此可以将对数几率记为输入特征值的线性表达式：
此处，p（y＝1|x）是在给定特征x的条件下，某一个样本属于类别1的条件概率。
我们在此的真正目的是预测某一样本属于特定类别的概率，它是logit函数的反函数，也称作logistic函数，由于它的图像呈S形，因此有时也简称为sigmoid函数：
这里的z为净输入，也就是样本特征与权重的线性组合，其计算方式为：
我们来绘制一下自变量取值介于区间[-7,7]的sigmoid函数的图像：
执行上述代码，将会呈现一个S形（sigmoidal）曲线：
可以看到，当z趋向于无穷大（z→∞）时，φ（z）趋近于1，这是由于e-z在z值极大的情况下其值变得极小。类似地，当z趋向于负无穷（z→-∞）时，φ（z）趋近于0，这是由于此时分母越来越大的结果。由此，可以得出结论：sigmoid函数以实数值作为输入并将其映射到[0,1]区间，其拐点位于φ（z）＝0.5处。
为了对逻辑斯谛回归模型有个直观的认识，我们可以将其与第2章介绍的Adaline联系起来。在Adaline中，我们使用恒等函数φ（z）＝z作为激励函数。而在逻辑斯谛回归中，只是简单地将前面提及的sigmoid函数作为激励函数，如下图所示：
在给定特征x及其权重w的情况下，sigmoid函数的输出给出了特定样本x属于类别1的概率φ（z）＝P（y＝1｜x;w）。例如，针对某一样本我们求得φ（z）＝0.8，这意味着该样本属于变色鸢尾的概率为80%。类似地，该样本属于山鸢尾的概率可计算为P（y＝0｜x;w）＝1-P（y＝1｜x;w）＝0.2，也就是20%。预测得到的概率可以通过一个量化器（单位阶跃函数）简单地转换为二元输出：
对照前面给出的sigmoid函数的图像，它其实相当于：
对于许多应用实践来说，我们不但对类标预测感兴趣，而且对事件属于某一类别的概率进行预测也非常有用。例如，将逻辑斯谛回归应用于天气预报，不仅要预测某天是否会下雨，还要推测出下雨有多大的可能性。同样，逻辑斯谛回归还可用于预测在出现某些症状的情况下，患者患有某种疾病的可能性，这也是逻辑斯谛回归在医疗领域得到广泛应用的原因。
[1] 某一事件发生与不发生的概率的比值。——译者注
3.3.2 通过逻辑斯谛回归模型的代价函数获得权重
我们已经学会了如何使用逻辑斯谛回归模型预测概率和类标。现在简要介绍一下模型的参数，例如这里的权重w。在上一章中，我们将其代价函数定义为误差平方和（sum-squared-error）：
通过最小化此代价函数，我们可以得到Adaline分类模型的权重w。为了推导出逻辑斯谛回归模型的代价函数，我们在构建逻辑斯谛回归模型时，需要先定义一个最大似然函数L，假定数据集中的每个样本都是相互独立的，其计算公式如下：
在实际应用中，很容易对此方程的（自然）对数进行最大化处理（求其极大值），故定义了对数似然函数：
首先，在似然函数值非常小的时候，可能出现数值溢出的情况，使用对数函数降低了这种情况发生的可能性。其次，我们可以将各因子的连乘转换为和的形式，利用微积分中的方法，通过加法转换技巧可以更容易地对函数求导。
现在可以通过梯度上升等优化算法最大化似然函数。或者，改写一下对数似然函数作为代价函数J，这样就可以使用第2章中的梯度下降做最小化处理了。
为了更好地理解这一代价函数，先了解一下如何计算单个样本实例的成本：
通过上述公式可以发现：如果y＝0，则第一项为0；如果y＝1，则第二项为0：
下图解释了在不同φ（z）值时对单一示例样本进行分类的代价：
可以看到，如果将样本正确划分到类别1中，代价将趋近于0（实线）。类似地，如果正确将样本划分到类别0中，y轴所代表的代价也将趋近于0（虚线）。然而，如果分类错误，代价将趋近于无穷。这也就意味着错误预测带来的代价将越来越大。
3.3.3 使用scikit-learn训练逻辑斯谛回归模型
如果想要自己编写代码实现逻辑斯谛回归，只要将第2章中的代价函数J替换为下面的代价函数：
该函数通过计算每次迭代过程中训练所有样本的成本，最终得到一个可用的逻辑斯谛回归模型。然而，由于scikit-learn已经有现成的经过高度优化的逻辑斯谛算法，而且还支持多类别分类，因此，我们不再尝试自己实现算法，转而使用sklearn.linear_model.LogisticRegression类来完成，同时使用我们已经非常熟悉的fit方法在鸢尾花训练数据集上训练模型。
在训练集上对模型进行训练后，我们在二维图像中绘制了决策区域、训练样本和测试样本，如下图所示：
分析前面用来训练LogisticRegression模型的代码，你也许会思考：“那个神秘的参数C代表什么？”下一节会先介绍一下过拟合和正则化的概念，然后再来讨论这个神秘的参数。
此外，可以通过predict_proba方法来预测样本属于某一类别的概率。例如，可以预测第一个样本属于各个类别的概率：
通过此代码可得到如下数组：
此数组表明模型预测此样本属于Iris-Virginica的概率为93.7%，属于Iris-Versicolor的概率为6.3%。
可以证明，逻辑斯谛回归中的回归系数更新用到的梯度下降本质上与第2章中的公式是相同的。首先，计算对数似然函数对第j个权重的偏导：
在进入下一步之前，先计算一下sigmoid函数的偏导：
我们的目标是求得能够使对数似然函数最大化的权重值，在此需按如下公式更新所有权重：
由于我们是同时更新所有的权重的，因此可以将更新规则记为：
其中，Δw定义为：
由于最大化对数似然函数等价于最小化前面定义的代价函数J，因此可以将梯度下降的更新规则定义为：
这等价于第2章中的梯度下降规则。
3.3.4 通过正则化解决过拟合问题
过拟合是机器学习中的常见问题，它是指模型在训练数据集上表现良好，但是用于未知数据（测试数据）时性能不佳。如果一个模型出现了过拟合问题，我们也说此模型有高方差，这有可能是因为使用了相关数据中过多的参数，从而使得模型变得过于复杂。同样，模型也可能面临欠拟合（高偏差）问题，这意味着模型过于简单，无法发现训练数据集中隐含的模式，这也会使得模型应用于未知数据时性能不佳。
虽然我们目前只介绍了分类中的线性模型，但对于过拟合与欠拟合问题，最好使用更加复杂的非线性决策边界来阐明，如下图所示：
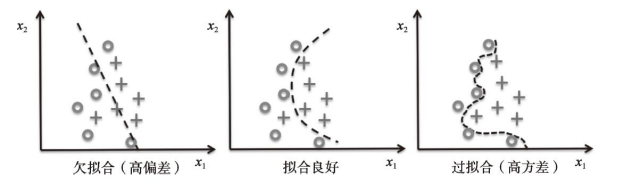
如果我们多次重复训练一个模型，如使用训练数据集中不同的子集，方差可以用来衡量模型对特定样本实例预测的一致性（或者说变化）。可以说模型对训练数据中的随机性是敏感的。相反，当我们在不同的训练数据集上多次重建模型时，偏差可以从总体上衡量预测值与实际值之间的差异；偏差并不是由样本的随机性导致的，它衡量的是系统误差。
偏差-方差权衡（bias-variance tradeoff）就是通过正则化调整模型的复杂度。正则化是解决共线性（特征间高度相关）的一个很有用的方法，它可以过滤掉滤数据中的噪声，并最终防止过拟合。正则化背后的概念是引入额外的信息（偏差）来对极端参数权重做出惩罚。最常用的正则化形式称为L2正则化（L2 regularization），它有时也称作L2收缩（L2 shrinkage）或权重衰减（weight decay），可写作：
其中，λ为正则化系数。
特征缩放（如标准化等）之所以重要，其中一个原因就是正则化。为了使得正则化起作用，需要确保所有特征的衡量标准保持统一。
使用正则化方法时λ，我们只需在逻辑斯谛回归的代价函数中加入正则化项，以降低回归系数带来的副作用：
通过正则化系数，保持权值较小时，我们就可以控制模型与训练数据的拟合程度。增加λ的值，可以增强正则化的强度。
前面用到了scikit-learn库中的LogisticRegression类，其中的参数C来自下一小节要介绍的支持向量机中的约定，它是正则化系数的倒数：
由此，我们可以将逻辑斯谛回归中经过正则化的代价函数写作：
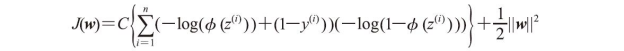
因此，减小正则化参数倒数C的值相当于增加正则化的强度，这可以通过绘制对两个权重系数进行L2正则化后的图像予以展示：
执行上述代码，我们使用不同的逆正则化参数C拟合了10个逻辑斯谛回归模型。出于演示的目的，我们仅仅记录了类别2区别于其他类别的权重系数。请牢记，我们使用OvR技术来实现多类别分类。
通过结果图像可以看到，如果我们减小参数C的值，也就是增加正则化项的强度，可以导致权重系数逐渐收缩。
由于深入讲解每个分类算法的细节已经超出了本书的讨论范围，因此强烈建议读者阅读Scott Menard博士的书籍（Logistic Regression:From Introductory to Advanced Concepts and Applications,Sage Publications）以了解更多关于逻辑斯谛回归的内容。