11.1 使用k-means算法对相似对象进行分组
本节将讨论一种最流行的聚类算法：k-means算法，它在学术领域及业界都得到了广泛应用。聚类（或称为聚类分析）是一种可以找到相似对象群组的技术，与组间对象相比，组内对象之间具有更高的相似度。聚类在商业领域的应用包括：按照不同主题对文档、音乐、电影等进行分组，或基于常见的购买行为，发现有相同兴趣爱好的顾客，并以此构建推荐引擎。
读者稍后将看到，与其他聚类算法相比，k-means算法易于实现，且具有很高的计算效率，这也许就是它得到广泛使用的原因。k-means算法是基于原型的聚类。在本章的后续内容中，我们还将讨论另外两种聚类：层次（hierarchical）聚类和基于密度（density-based）的聚类。基于原型的聚类意味着每个簇都对应一个原型，它可以是一些具有连续型特征的相似点的中心点（centroid）（平均值），或者是类别特征情况下相似点的众数（medoid）——最典型或是出现频率最高的点。虽然k-means算法可以高效识别球形簇，但是此算法的缺点在于必须事先指定先验的簇数量k。如果k值选择不当，则可能导致聚类效果不佳。本章后续还将讨论肘（elbow）方法和轮廓图（silhouette plot），它们可以用来评估聚类效果，并帮助我们选出最优k值。
尽管k-means聚类适用于高维数据，但出于可视化需要，我们将使用一个二维数据集的例子进行演示：
我们刚才创建的数据集中包含150个随机生成的点，它们大致分为三个高密度区域，其二维散点图如下：
在聚类算法的实际应用中，我们没有任何关于这些样本的类别基础信息；否则算法就要划分到监督学习的范畴了。由此，我们的目标就是根据样本自身特征的相似性对其进行分组，对此可采用k-means算法，具体有如下四个步骤：
1）从样本点中随机选择k个点作为初始簇中心。
2）将每个样本点划分到距离它最近的中心点μ（j）,j∈{1,…,k}所代表的簇中。
3）用各簇中所有样本的中心点替代原有的中心点。
4）重复步骤2和3，直到中心点不变或者达到预定迭代次数时，算法终止。
现在面临的一个问题就是：如何度量对象之间的相似性？我们可以将相似性定义为距离的倒数，在m维空间中，对于特征取值为连续型实数的聚类分析来说，常用的距离度量标准是欧几里得距离的平方：
请注意，在前面的公式中，下标索引j为样本点x和y的第j个维度（特征列）。本节后续内容将分别使用上标i和j来代表样本索引和簇索引。
基于欧几里得度量标准，我们可以将k-means算法描述为一个简单的优化问题，通过迭代使得簇内误差平方和（within-cluster sum of squared errors，SSE）最小，也称作簇惯性（cluster intertia）。
其中，μ（j）为簇j的中心点，如果样本x（i）属于簇j，则有w（i,j）＝1，否则w（i,j）＝0。
至此，我们已经知道了简单k-means算法的工作原理，现在借助scikit-learn中的KMeans类将k-means算法应用于我们的示例数据集：
使用上述代码，我们将簇数量设定为3个；指定先验的簇数量是k-means算法的一个缺陷，设置n_init＝10，程序能够基于不同的随机初始中心点独立运行算法10次，并从中选择SSE最小的作为最终模型。通过max_iter参数，指定算法每轮运行的迭代次数（在本例中为300次）。请注意，在scikit-learn对k-means算法的实现中，如果模型收敛了，即使未达到预定迭代次数，算法也将终止。
不过，在k-means算法的某轮迭代中，可能会发生无法收敛的情况，特别是当我们设置了较大的max_iter值时，更有可能产生此类问题。解决收敛问题的一个方法就是为tol参数设置一个较大的值，此参数控制对簇内误差平方和的容忍度，此容忍度用于判定算法是否收敛。在上述代码中，我们设置的容忍度为1e-04（0.0001）。
11.1.1 k-means++
到目前为止，我们已经讨论了经典的k-means算法，它使用随机点作为初始中心点，若初始中心点选择不当，有可能会导致簇效果不佳或产生收敛速度慢等问题。解决此问题的一种方案就是在数据集上多次运行k-means算法，并根据误差平方和（SSE）选择性能最好的模型。另一种方案就是使用k-means++算法让初始中心点彼此尽可能远离，相比传统k-means算法，它能够产生更好、更一致的结果。[1]
k-means++算法的初始化过程可以概括如下：
1）初始化一个空的集合M，用于存储选定的k个中心点。
2）从输入样本中随机选定第一个中心点μ（j），并将其加入到集合M中。
3）对于集合M之外的任一样本点x（i），通过计算找到与其平方距离最小的样本d（x（i）,M）2。
4）使用加权概率分布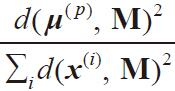
来随机选择下一个中心点μ（p）。
5）重复步骤2、3，直到选定k个中心点。
6）基于选定的中心点执行k-means算法。
通过scikit-learn的KMeans对象来实现k-means++算法，只需将init参数的值random替换为k-means++（默认值）即可。
k-means算法还有另一个问题，就是一个或多个簇的结果可能为空。但k-medoids或者模糊C-means算法中不存在这种问题，我们将在下一小节讨论这两种算法。不过，此问题在当前scikit-learn实现的k-means算法中是存在的。如果某个簇为空，算法将搜索距离空簇中心点最远的样本，然后将此最远样本点作为中心点。
当我们使用欧几里得距离作为度量标准将k-means算法应用到真实数据中时，需要保证所有特征值的范围处于相同尺度，必要时可使用z-score标准化或最小-最大缩放方法对数据进行预处理。
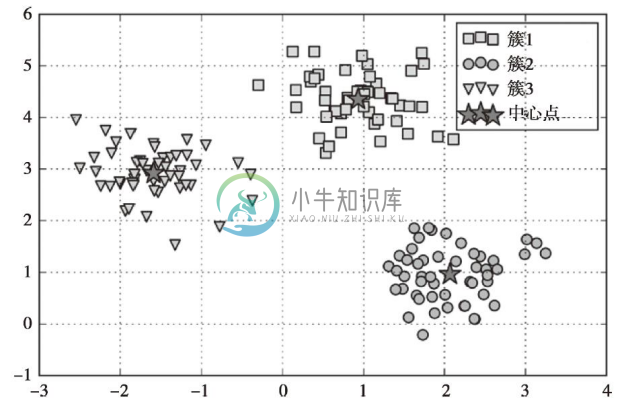
我们已经将簇结果存储在y_km中，并且讨论了k-means算法面临的挑战，现在对k-means算法的簇结果及其相应的簇中心做可视化展示。簇中心保存在KMeans对象的centers_属性中：
在下面的散点图中，我们可以看到，通过k-means算法得到的3个中心点位于各球状簇的圆心位置，在此数据集上，分组结果看起来是合理的。
虽然k-means算法在这一简单数据集上运行良好，但我们还要注意k-means算法面临的一些挑战。k-means的缺点之一就是我们必须指定一个先验的簇数量k，但在实际应用中，簇数量并非总是显而易见的，特别当我们面对的是一个无法可视化展现的高维数据集。k-means的另一个特点就是簇不可重叠，也不可分层，并且假定每个簇至少会有一个样本。
[1] D. Arthur and S. Vassilvitskii. k-means++: The Advantages of Careful Seeding. In Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms, pages 1027-1035. Society for Industrial and Applied Mathematics, 2007.
11.1.2 硬聚类与软聚类
硬聚类（hard clustering）指的是数据集中每个样本只能划至一个簇的算法，例如我们在上一小节中讨论过的k-means算法。相反，软聚类（soft clustering，有时也称作模糊聚类（fuzzy clustering））算法可以将一个样本划分到一个或者多个簇。一个常见的软聚类算法是模糊C-means（fuzzy C-means，FCM）算法（也称为soft k-means或者fuzzy k-means）。关于软聚类的最初构想可以追溯到20世纪70年代，当时Joseph C.Dunn第一个提出了模糊聚类的早期版本，以提高k-means的性能[1]。10年之后，James C.Bedzek发表了他对模糊聚类算法进行改进的研究成果，即FCM算法[2]。
FCM的处理过程与k-means十分相似。但是，我们使用每个样本点隶属于各簇的概率来替代硬聚类的划分。在k-means中，我们使用二进制稀疏向量来表示各簇所含样本：
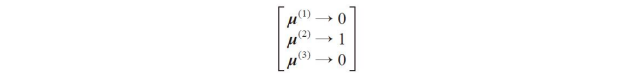
其中，位置索引的值为1表示样本属于簇中心μ（j）所在的簇（假定k＝3，则j∈{1,2,3}）。相反，FMC中的成员隶属向量可以表示如下：
这里，每个值都在区间[0,1]内，代表样本属于相应簇中心所在簇的概率。对于给定样本，其隶属于各簇的概率之和为1。与k-means算法类似，我们可以将FCM算法总结为四个核心步骤：
1）指定k个中心点，并随机将每个样本点划分至某个簇。
2）计算各簇中心μ（j）,j∈{1,…,k}。
3）更新各样本点所属簇的成员隶属度。
4）重复步骤2、3，直到各样本点所属簇成员隶属度不变，或是达到用户自定义的容差阈值或最大迭代次数。
可以将FCM的目标函数简写为Jm，它看起来与k-means中需要进行最小化计算的簇内误差平方和（within cluster sum-squared-error）很相似：
不过请注意：此处的成员隶属度w（i,j）不同于k-means算法中的二进制值（w（i,j）∈{0,1}），它是一个实数，表示样本隶属于某个簇的概率（w（i,j）∈[0,1]）。读者也许注意到了，我们在w（i,j）中增加了额外的一个指数m，一般情况下其取值范围是大于等于1的整数（通常m＝2），也称为模糊系数（fuzziness coefficient，或直接就叫模糊器（fuzzzifier）），用来控制模糊的程度。模糊聚类中，m的值越大则成员隶属度w（i,j）越小。样本点属于某个簇的概率计算公式如下：
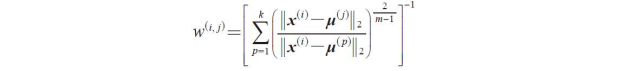
如同前面的k-means例子，在此依旧使用3个簇中心，可通过以下方式计算出样本x（i）属于簇μ（j）的隶属度：
以样本属于特定簇的隶属度为权重，此簇中心μ（j）可以通过所有样本的加权均值计算得到：
仅就计算样本数据簇的隶属度公式来说，直观上看，FCM的单次迭代计算成本比k-means的要高，但是FCM通常只需较少的迭代次数便能收敛。遗憾的是，scikit-learn目前还未实现FCM算法。不过，正如Soumi Ghosh与Sanjay K.Dubey的研究[3]所述，实际应用中k-means和FCM算法通常会得到较为相似的结果。
[1] J. C. Dunn. A Fuzzy Relative of the Isodata Process and its Use in Detecting Compact Well-separated Clusters. 1973.
[2] J. C. Bezdek. Pattern Recognition with Fuzzy Objective Function Algorithms. Springer Science & Business Media, 2013.
[3] S. Ghosh and S. K. Dubey. Comparative Analysis of k-means and Fuzzy c-means Algorithms. IJACSA, 4:35-38, 2013.
11.1.3 使用肘方法确定簇的最佳数量
无监督学习中存在一个问题，就是我们并不知道问题的确切答案。由于没有数据集样本类标的确切数据，所以我们无法在无监督学习中使用第6章中用来评估监督学习模型性能的相关技术。因此，为了对聚类效果进行定量分析，我们需要使用模型内部的固有度量来比较不同k-means聚类结果的性能，例如本章先前讨论过的簇内误差平方和（即聚类偏差）。在完成KMeans模型的拟合后，簇内误差平方和可以通过inertia属性来访问，因此，我们无需再次计算就可直接拿来使用。
基于簇内误差平方和，我们可使用图形工具，即所谓的肘方法，针对给定任务估计出最优的簇数量k。直观地看，增加k的值可以降低聚类偏差。这是因为样本会更加接近其所在簇的中心点。肘方法的基本理念就是找出聚类偏差骤增时的k值，我们可以绘制出不同k值对应的聚类偏差图，以做更清晰的观察：
如下图所示，当k＝3时图案呈现了肘型，这表明对于此数据集来说，k＝3的确是一个好的选择：
11.1.4 通过轮廓图定量分析聚类质量
另一种评估聚类质量的定量分析方法是轮廓分析（silhouette analysis），此方法也可用于k-means之外的其他聚类方法。轮廓分析可以使用一个图形工具来度量簇中样本聚集的密集程度。通过如下三个步骤，我们可以计算数据集中单个样本的轮廓系数（silhouette coefficient）：
1）将某一样本x（i）与簇内其他点之间的平均距离看作是簇的内聚度a（i）。
2）将样本x（i）与其最近簇中所有点之间的平均距离看作是与下一最近簇的分离度b（i）。
3）将簇分离度与簇内聚度之差除以二者中的较大者得到轮廓系数，如下式所示：
轮廓系数的值介于-1到1之间。从上式可见，若簇内聚度与分离度相等（b（i）＝a（i）），则轮廓系数值为0。此外，由于b（i）衡量样本与其他簇内样本间的差异程度，而a（i）表示样本与簇内其他样本的相似程度，因此，如果b（i）>>a（i），我们可以近似得到一个值为1的理想的轮廓系数。
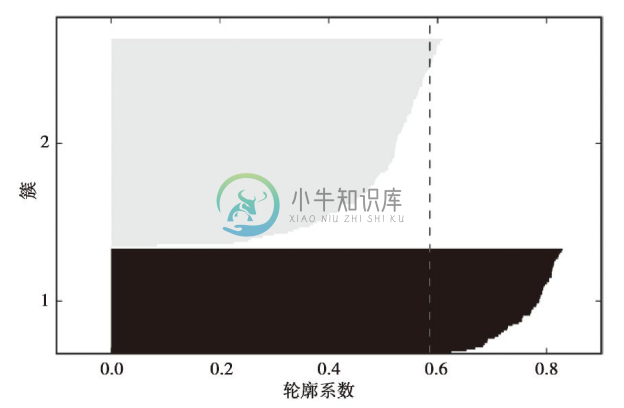
轮廓系数可通过scikit-learn中metric模块下的silhouette_samples计算得到，也可选择使用silhouette_scores。后者计算所有样本点的轮廓系数均值，等价于numpy.mean（silhouette_samples（…））。执行下面的代码，我们可以绘制出k＝3时k-means算法的轮廓系数图：
通过观察轮廓图，我们可以快速知晓不同簇的大小，而且能够判断出簇中是否包含异常点。
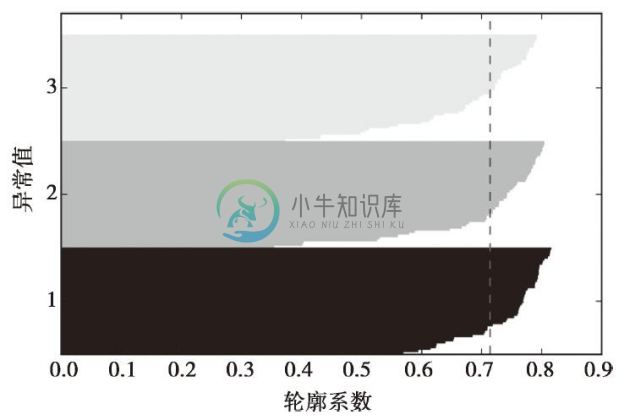
由上图可见，轮廓系数未接近0点，此指标显示聚类效果不错。此外，为了评判聚类效果的优劣，我们在图中增加了轮廓系数的平均值（虚线）。
为了解聚类效果不佳的轮廓图的形状，我们使用两个中心点来初始化k-means算法：
由下图可见，样本点形成了三个球状分组，其中一个中心点落在了两个球状分组的中间。尽管聚类结果看上去不是特别糟糕，但它并不是最合适的结果。
接下来，我们绘制轮库图对聚类结果进行评估。请记住，在实际应用中，我们常常处理的是高维数据，因此并不奢望使用二维散点图对数据集进行可视化。
由结果图像可见，轮廓具有明显不同的长度和宽度，这更进一步证明该聚类并非最优结果。
