python实现k-means聚类算法

k-means聚类算法

k-means是发现给定数据集的k个簇的算法，也就是将数据集聚合为k类的算法。

算法过程如下：
1）从N个文档随机选取K个文档作为质心
2）对剩余的每个文档测量其到每个质心的距离，并把它归到最近的质心的类，我们一般取欧几里得距离
3）重新计算已经得到的各个类的质心
4）迭代步骤（2）、（3）直至新的质心与原质心相等或迭代次数大于指定阈值，算法结束

算法实现

随机初始化k个质心，用dict保存质心的值以及被聚类到该簇中的所有data。

def initCent(dataSet , k):
 N = shape(dataSet)[1]
 cents = {}
 randIndex=[]
 #随机生成k个不重复的索引
 for i in range(k): 
 rand = random.randint(0,N)
 while rand in randIndex:
  rand = random.randint(0, N)
 randIndex.append(rand)
 #按索引取dataSet中的data作为质心
 for i in range(k):
 templist = []
 templist.append(dataSet[randIndex[i]])
 templist.append([dataSet[randIndex[i]]])
 cents[i] = templist
 return cents

对dataSet中的所有数据进行一次聚类。返回值cents为dict类型的数据，int类型的key，list类型的value。其中cents[i][0]为质心位置，cents[i][1]为存储该簇中所有data的列表。

#计算两个向量的欧氏距离
def calDist(X1 , X2):
 sum = 0
 for x1 , x2 in zip(X1 , X2):
 sum += (x1 - x2) ** 2
 return sum ** 0.5

#聚类
def doKmeans(dataSet , k , cents):
 #清空上一次迭代后的簇中元素，只记录质心
 for i in range(k):
 cents[i][1] = []
 for data in dataSet:
 no = 0#初始化簇标号
 minDist = sys.maxint#初始化data与k个质心的最短距离
 for i in range(k):
  dist = calDist(data , cents[i][0])
  if dist < minDist:
  minDist = dist
  no = i
 #找到距离最近的质心
 cents[no][1].append(data)
 #更新质心
 for i in range(k):
 for j in range(shape(dataSet)[0]):
  cents[i][0] = mean(cents[i][1],axis=0).tolist()
 return cents

k-means主方法

#判断两次聚类的结果是否相同
def isEqual(old , new):
 for i in range(len(old)):
 if(old[i] != new[i][0]):
  return 0
 return 1

#主方法
def kmeans_main(dataSet,k):
 cents = initCent(dataSet, k)
 for x in range(1000):
 oldcents = []
 #拷贝上一次迭代的结果
 for i in cents.keys():
  oldcents.append(cents[i][0])
 newcents = doKmeans(dataSet, k , cents)
 #若相邻两次迭代结果相同，算法结束
 if isEqual(oldcents , newcents)>0:
  break
 cents = newcents
 return cents

结果测试

数据集（虚构）

2 3 2.54
2 1 0.72
3 5 3.66
4 3 1.71
3.11 5.29 4.13
4.15 2 3.1
3.12 3.33 3.72
1.49 5 2.6
3 5 2.88
3.9 1.78 2.56
-2 3 5
3 1 0.4
-2 1 2.2
-3 0 1.7
-4 1 2
8 -1 0
2 3.2 7.1
1 3 5
2 4 3
0.1 2 5.4
2 0 5.54
2 1 1.72
3 5 2.66
1 8 1.71
5.11 1.29 4.13
7.15 2 7.1
1.12 5.33 4.72
6.49 4 3.6
4 8 6.88
1.9 5.78 6.56
-2 -3 2.5
1 -1 2.4
-2 1 3.2
-1 0 5.7
-2 3 2
1 -1 4
3 4.2 6.1
5 2 5
3 5.7 13
0.9 2.9 1.4

画图方法

def draw(cents):
 color = [ 'y', 'g', 'b']
 X = []
 Y = []
 Z = []
 fig = plt.figure()
 ax = Axes3D(fig)
 for i in cents.keys():
 X.append(cents[i][0][0])
 Y.append(cents[i][0][1])
 Z.append(cents[i][0][2])
 ax.scatter(X, Y, Z,alpha=0.4,marker='o',color='r', label=str(i))
 for i in cents.keys():
 X = []
 Y = []
 Z = []
 data = cents[i][1]
 for vec in data:
  X.append(vec[0])
  Y.append(vec[1])
  Z.append(vec[2])
 ax.scatter(X, Y, Z, alpha=0.4,marker='o', color=color[i], label=str(i),)
 plt.show()

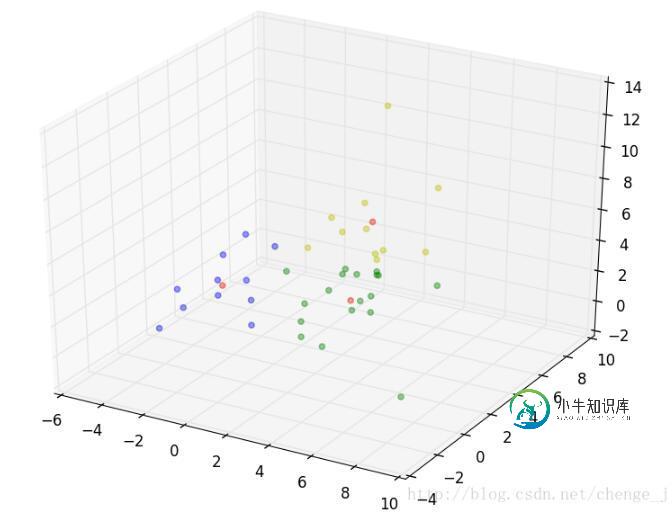
测试及结果展示（红点表示质心）

dataSet = loadDataSet("dataSet.txt")
cents = kmeans_main(dataSet , 3)
draw(cents)

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。