登录
当前位置： 首页 > 编程笔记 >

C语言中K-means算法实现代码

艾昊明
2023-03-14
本文向大家介绍C语言中K-means算法实现代码，包括了C语言中K-means算法实现代码的使用技巧和注意事项，需要的朋友参考一下

K-means算法是很典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

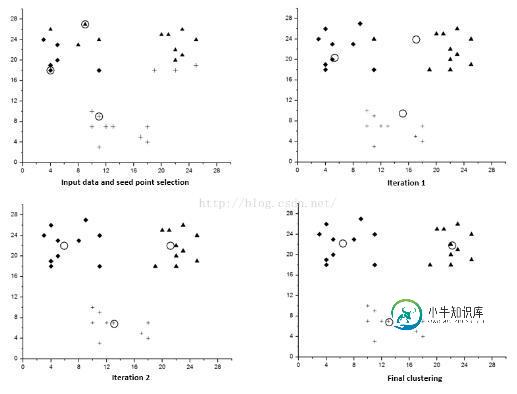
算法过程如下：

1）从N个样本随机选取K个样本作为质心
2）对剩余的每个样本测量其到每个质心的距离，并把它归到最近的质心的类
3）重新计算已经得到的各个类的质心
4）迭代2～3步直至新的质心与原质心相等或小于指定阈值，算法结束

#include<stdio.h> 
#include<stdlib.h> 
#include<string.h> 
#include<time.h> 
#include<math.h> 
 
#define DIMENSIOM  2    //目前只是处理2维的数据 
#define MAX_ROUND_TIME 100   //最大的聚类次数 
 
typedef struct Item{ 
  int dimension_1;    //用于存放第一维的数据 
  int dimension_2;    //用于存放第二维的数据 
  int clusterID;     //用于存放该item的cluster center是谁 
}Item; 
Item* data; 
 
typedef struct ClusterCenter{ 
  double dimension_1; 
  double dimension_2; 
  int clusterID; 
}ClusterCenter; 
ClusterCenter* cluster_center_new; 
 
int isContinue; 
 
int* cluster_center;    //记录center 
double* distanceFromCenter; //记录一个“点”到所有center的距离 
int data_size; 
char filename[200]; 
int cluster_count; 
 
void initial(); 
void readDataFromFile(); 
void initial_cluster(); 
void calculateDistance_ToOneCenter(int itemID, int centerID, int count); 
void calculateDistance_ToAllCenter(int itemID); 
void partition_forOneItem(int itemID); 
void partition_forAllItem_OneCluster(int round); 
void calculate_clusterCenter(int round); 
void K_means(); 
void writeClusterDataToFile(int round); 
void writeClusterCenterToFile(int round); 
void compareNew_OldClusterCenter(double* new_X_Y); 
void test_1(); 
 
int main(int argc, char* argv[]){ 
  if( argc != 4 ) 
  { 
    printf("This application need other parameter to run:" 
        "\n\t\tthe first is the size of data set," 
        "\n\t\tthe second is the file name that contain data" 
        "\n\t\tthe third indicate the cluster_count" 
        "\n"); 
    exit(0); 
  } 
  srand((unsigned)time(NULL)); 
  data_size = atoi(argv[1]); 
  strcat(filename, argv[2]); 
  cluster_count = atoi(argv[3]); 
 
  initial(); 
  readDataFromFile(); 
  initial_cluster(); 
  //test_1(); 
  //partition_forAllItem_OneCluster(); 
  //calculate_clusterCenter(); 
  K_means(); 
  return 0; 
} 
 
/* 
 * 对涉及到的二维动态数组根据main函数中传入的参数分配空间 
 * */ 
void initial(){ 
  data = (Item*)malloc(sizeof(struct Item) * (data_size + 1)); 
  if( !data ) 
  { 
    printf("malloc error:data!"); 
    exit(0); 
  } 
  cluster_center = (int*)malloc(sizeof(int) * (cluster_count + 1)); 
  if( !cluster_center ) 
  { 
    printf("malloc error:cluster_center!\n"); 
    exit(0); 
  } 
  distanceFromCenter = (double*)malloc(sizeof(double) * (cluster_count + 1)); 
  if( !distanceFromCenter ) 
  { 
    printf("malloc error: distanceFromCenter!\n"); 
    exit(0); 
  } 
  cluster_center_new = (ClusterCenter*)malloc(sizeof(struct ClusterCenter) * (cluster_count + 1)); 
  if( !cluster_center_new ) 
  { 
    printf("malloc cluster center new error!\n"); 
    exit(0); 
  } 
} 
 
/* 
 * 从文件中读入x和y数据 
 * */ 
void readDataFromFile(){ 
  FILE* fread; 
  if( NULL == (fread = fopen(filename, "r"))) 
  { 
    printf("open file(%s) error!\n", filename); 
    exit(0); 
  } 
  int row; 
  for( row = 1; row <= data_size; row++ ) 
  { 
    if( 2 != fscanf(fread, "%d %d ", &data[row].dimension_1, &data[row].dimension_2)) 
    { 
      printf("fscanf error: %d\n", row); 
    } 
    data[row].clusterID = 0; 
  } 
} 
 
/* 
 * 根据从主函数中传入的@cluster_count(聚类的个数)来随机的选择@cluster_count个 
 * 初始的聚类的起点 
 * */ 
 
void initial_cluster(){ 
  //辅助产生不重复的数 
  int* auxiliary; 
  int i; 
  auxiliary = (int*)malloc(sizeof(int) * (data_size + 1)); 
  if( !auxiliary ) 
  { 
    printf("malloc error: auxiliary"); 
    exit(0); 
  } 
  for( i = 1; i <= data_size; i++ ) 
  { 
    auxiliary[i] = i; 
  } 
   
  //产生初始化的cluster_count个聚类 
  int length = data_size; 
  int random; 
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    random = rand()%length + 1; 
    //printf("%d \n", auxiliary[random]); 
    //data[auxiliary[random]].clusterID = auxiliary[random]; 
    cluster_center[i] = auxiliary[random]; 
    auxiliary[random] = auxiliary[length--]; 
  } 
   
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    cluster_center_new[i].dimension_1 = data[cluster_center[i]].dimension_1; 
    cluster_center_new[i].dimension_2 = data[cluster_center[i]].dimension_2; 
    cluster_center_new[i].clusterID = i; 
    data[cluster_center[i]].clusterID = i; 
  } 
} 
 
/* 
 * 计算一个点(还没有划分到cluster center的点)到一个cluster center的distance 
 *   @itemID:  不属于任何cluster中的点 
 *   @centerID: center的ID 
 *   @count:   表明在计算的是itemID到第几个@center的distance，并且指明了结果放在distanceFromCenter的第几号元素 
 * */ 
void calculateDistance_ToOneCenter(int itemID,int centerID){ 
  distanceFromCenter[centerID] = sqrt( (data[itemID].dimension_1-cluster_center_new[centerID].dimension_1)*(double)(data[itemID].dimension_1-cluster_center_new[centerID].dimension_1) + (double)(data[itemID].dimension_2-cluster_center_new[centerID].dimension_2) * (data[itemID].dimension_2-cluster_center_new[centerID].dimension_2) ); 
} 
 
/* 
 * 计算一个点(还没有划分到cluster center的点)到每个cluster center的distance 
 * */ 
void calculateDistance_ToAllCenter(int itemID){ 
  int i; 
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    calculateDistance_ToOneCenter(itemID, i); 
  } 
} 
 
void test_1() 
{ 
  calculateDistance_ToAllCenter(3); 
  int i; 
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    printf("%f ", distanceFromCenter[i]); 
  } 
} 
 
/* 
 * 在得到任一的点(不属于任一cluster的)到每一个cluster center的distance之后，决定它属于哪一个cluster center,即取距离最小的 
 *   函数功能：得到一个item所属的cluster center 
 * */ 
void partition_forOneItem(int itemID){ 
  //操作对象是 distanceFromCenter和cluster_center 
  int i; 
  int min_index = 1; 
  double min_value = distanceFromCenter[1]; 
  for( i = 2; i <= cluster_count; i++ ) 
  { 
    if( distanceFromCenter[i] < min_value ) 
    { 
      min_value = distanceFromCenter[i]; 
      min_index = i; 
    } 
  } 
 
  data[itemID].clusterID = cluster_center_new[min_index].clusterID; 
} 
 
/* 
 * 得到所有的item所属于的cluster center , 在一轮的聚类中 
 * */ 
void partition_forAllItem_OneCluster(int round){        //changed!!!!!!!!!!!!!!!!!!!!!!!! 
  int i; 
  for( i = 1; i <= data_size; i++ ) 
  { 
    if( data[i].clusterID != 0 ) 
      continue; 
    else 
    { 
      calculateDistance_ToAllCenter(i);  //计算i到所有center的distance 
      partition_forOneItem(i);    //根据distance对i进行partition 
    } 
  } 
 
  //把聚类得到的数据写入到文件中 
  writeClusterDataToFile(round); 
} 
 
/* 
 * 将聚类得到的数据写入到文件中，每一个类写入一个文件中 
 *   @round: 表明在进行第几轮的cluster，该参数的另一个作用是指定了文件名字中的第一个项. 
 * */ 
void writeClusterDataToFile(int round){ 
  int i; 
  char filename[200]; 
  FILE** file; 
  file = (FILE**)malloc(sizeof(FILE*) * (cluster_count + 1)); 
  if( !file ) 
  { 
    printf("malloc file error!\n"); 
    exit(0); 
  } 
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    sprintf(filename, ".//ClusterProcess//round%d_cluster%d.data", round, i); 
    if( NULL == (file[i] = fopen(filename, "w"))) 
    { 
      printf("file open(%s) error!", filename); 
      exit(0); 
    } 
  } 
   
  for( i = 1; i <= data_size; i++ ) 
  { 
    //sprintf(filename, ".//ClusterProcess//round%d_cluster%d.data", round, data[i].clusterID); 
    fprintf(file[data[i].clusterID], "%d\t%d\n", data[i].dimension_1, data[i].dimension_2); 
  } 
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    //sprintf(filename, ".//ClusterProcess//round%d_cluster%d.data", round, i); 
    fclose(file[i]); 
  } 
} 
 
/* 
 * 重新计算新的cluster center 
 * */ 
void calculate_clusterCenter(int round){          //changed!!!!!!!!!!!!!!!!!!!!!! 
  int i; 
  double* new_X_Y;  /* 
          用来计算和保存新的cluster center的值，同样的，0号元素不用。1,2号元素分别用来 
          存放第一个聚类的所有的项的x和y的累加和。3,4号元素分别用来存放第二个聚类的所有 
          的项的x和y的累加和...... 
        */ 
  new_X_Y = (double*)malloc(sizeof(double) * (2 * cluster_count + 1)); 
  if( !new_X_Y ) 
  { 
    printf("malloc error: new_X_Y!\n"); 
    exit(0); 
  } 
  //初始化为0 
  for( i = 1; i <= 2*cluster_count; i++ ) 
    new_X_Y[i] = 0.0; 
 
  //用来统计属于各个cluster的item的个数 
  int* counter; 
  counter = (int*)malloc(sizeof(int) * (cluster_count + 1)); 
  if( !counter ) 
  { 
    printf("malloc error: counter\n"); 
    exit(0); 
  } 
  //初始化为0 
  for( i = 1; i <= cluster_count; i++ ) 
    counter[i] = 0; 
 
  for( i = 1; i <= data_size; i++ ) 
  { 
    new_X_Y[data[i].clusterID * 2 - 1] += data[i].dimension_1; 
    new_X_Y[data[i].clusterID * 2] += data[i].dimension_2; 
    counter[data[i].clusterID]++; 
  } 
 
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    new_X_Y[2 * i - 1] = new_X_Y[2 * i - 1] / (double)(counter[i]); 
    new_X_Y[2 * i] = new_X_Y[2 * i] / (double)(counter[i]); 
  } 
   
  //要将cluster center的值保存在文件中，后续作图 
  writeClusterCenterToFile(round); 
   
  /* 
   * 在这里比较一下新的和旧的cluster center值的差别。如果是相等的，则停止K-means算法。 
   * */ 
  compareNew_OldClusterCenter(new_X_Y); 
 
  //将新的cluster center的值放入cluster_center_new 
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    cluster_center_new[i].dimension_1 = new_X_Y[2 * i - 1]; 
    cluster_center_new[i].dimension_2 = new_X_Y[2 * i]; 
    cluster_center_new[i].clusterID = i; 
  } 
  free(new_X_Y); 
  free(counter); 
 
  //在重新计算了新的cluster center之后，意味着我们要重新来为每一个Item进行聚类，所以data中用于表示聚类ID的clusterID 
  //要都重新置为0。 
  for( i = 1; i <= data_size; i++ ) 
  { 
    data[i].clusterID = 0; 
  } 
} 
 
/* 
 * 将得到的新的cluster_count个cluster center的值保存在文件中。以便于观察聚类的过程。 
 * */ 
void writeClusterCenterToFile(int round){ 
  FILE* file; 
  int i; 
  char filename[200]; 
  sprintf(filename, ".//ClusterProcess//round%d_clusterCenter.data", round); 
  if( NULL == (file = fopen(filename, "w"))) 
  { 
    printf("open file(%s) error!\n", filename); 
    exit(0); 
  } 
 
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    fprintf(file, "%f\t%f\n", cluster_center_new[i].dimension_1, cluster_center_new[i].dimension_2); 
  } 
 
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    fclose(file); 
  } 
} 
 
/* 
 * 比较新旧的cluster center的差异 
 * */ 
void compareNew_OldClusterCenter(double* new_X_Y){ 
  int i; 
  isContinue = 0;       //等于0表示的是不要继续 
  for( i = 1; i <= cluster_count; i++ ) 
  { 
    if( new_X_Y[2 * i - 1] != cluster_center_new[i].dimension_1 || new_X_Y[2 * i] != cluster_center_new[i].dimension_2) 
    { 
      isContinue = 1;   //要继续 
      break; 
    } 
  } 
} 
 
/************************************************************************************************ 
 *         K-means算法            *    
 ***********************************************************************************************/ 
void K_means(){ 
  int times_cluster; 
  for( times_cluster = 1; times_cluster <= MAX_ROUND_TIME; times_cluster++ ) 
  { 
    printf("\n            times : %d             \n", times_cluster); 
    partition_forAllItem_OneCluster(times_cluster); 
    calculate_clusterCenter(times_cluster); 
    if( 0 == isContinue ) 
    { 
      break; 
      //printf("\n\nthe application can stop!\n\n"); 
    } 
  } 
}

 

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。

 类似资料：
  • C语言实现K-Means算法

    本文向大家介绍C语言实现K-Means算法，包括了C语言实现K-Means算法的使用技巧和注意事项，需要的朋友参考一下 一、聚类和聚类算法 聚类，就是将数据对象划分成若干个类，在同一个类中的对象具有较高的相似度，而不同的类相似度较小。聚类算法将数据集合进行划分，分成彼此相互联系的若干类，以此实现对数据的深入分析和数据价值挖掘的初步处理阶段。例如在现代商业领域，聚类分析算法可以从庞大的数据集合中对消

  • k-means 聚类算法与Python实现代码

    本文向大家介绍k-means 聚类算法与Python实现代码，包括了k-means 聚类算法与Python实现代码的使用技巧和注意事项，需要的朋友参考一下 k-means 聚类算法思想先随机选择k个聚类中心，把集合里的元素与最近的聚类中心聚为一类，得到一次聚类，再把每一个类的均值作为新的聚类中心重新聚类，迭代n次得到最终结果分步解析 一、初始化聚类中心 首先随机选择集合里的一个元素作为第一个聚类中

  • python实现k-means聚类算法

    本文向大家介绍python实现k-means聚类算法，包括了python实现k-means聚类算法的使用技巧和注意事项，需要的朋友参考一下 k-means聚类算法 k-means是发现给定数据集的k个簇的算法，也就是将数据集聚合为k类的算法。 算法过程如下： 1）从N个文档随机选取K个文档作为质心 2）对剩余的每个文档测量其到每个质心的距离，并把它归到最近的质心的类，我们一般取欧几里得距离 3）重

  • k-means算法流程

    本文向大家介绍k-means算法流程相关面试题，主要包含被问及k-means算法流程时的应答技巧和注意事项，需要的朋友参考一下 参考回答： 从数据集中随机选择k个聚类样本作为初始的聚类中心,然后计算数据集中每个样本到这k个聚类中心的距离,并将此样本分到距离最小的聚类中心所对应的类中。将所有样本归类后,对于每个类别重新计算每个类别的聚类中心即每个类中所有样本的质心,重复以上操作直到聚类中心不变为止。

  • 聚类 - k-means算法

      本文会介绍一般的k-means算法、k-means++算法以及基于k-means++算法的k-means||算法。在spark ml，已经实现了k-means算法以及k-means||算法。 本文首先会介绍这三个算法的原理，然后在了解原理的基础上分析spark中的实现代码。 1 k-means算法原理分析   k-means算法是聚类分析中使用最广泛的算法之一。它把n个对象根据它们的属性分为k

  • C语言实现的PNPoly算法代码例子

    本文向大家介绍C语言实现的PNPoly算法代码例子，包括了C语言实现的PNPoly算法代码例子的使用技巧和注意事项，需要的朋友参考一下 写C语言的实验用到的一个算法，判断一个点是否在多边形的内部。C的代码如下： 其中nvert是多边形顶点的个数，vertx和verty分别是多边形顶点横、纵坐标的数组，textx和testy是待测点的坐标。这个算法是由W. Randolph Franklin提出的，

相关阅读

C语言实现的PNPoly算法代码例子马尔可夫链算法（markov算法）的awk、C++、C语言实现代码C语言实现九大排序算法的实例代码C语言 选择排序算法详解及实现代码C语言实现冒泡排序算法

相关文章

C语言条件运算符C语言逻辑运算符C语言关系运算符C语言加减乘除运算C语言指针变量的运算

相关问答

C语言中正弦函数不工作的实现基于CLRS的合并排序算法介绍，带反转计数，C语言实现C语言中三维直接卷积实现的优化如何降低c语言中算法的时间复杂度？如何在ANTLR中实现C语言解析器的lexer hack

相关工具

算法(Rust语言描述)C 语言入门教程《Swift语言》中文版神语言Shen语言

相关文档

C/C++ 语言参考通过实例学习 C 语言C 语言教程学习 C 语言C 语言编程透视
快捷导航： 新手教程 算法原理 架构设计 Java进阶 数据库进阶 大厂专栏 面试经验 编程笔记 编程问答 所有专题 文档资料 工具软件 电子书籍 小牛导航
在线工具： 房贷计算器 个税计算器 Linux命令查询 Json格式化 正则表达式 颜色转换 AES加解密 SHA1加密 MD5加密 毒鸡汤 字数统计 随机密码生成 进制转换 Base64编解码 励志句子
Copyright © 2019-2024 小牛知识库@xnip.cn. All Rights Reserved.