5.1 无监督数据降维技术——主成分分析
与特征选择类似,我们可以使用特征抽取来减少数据集中特征的数量。不过,当使用序列后向选择等特征选择算法时,能够保持数据的原始特征,而特征抽取算法则会将数据转换或者映射到一个新的特征空间。基于降维在数据预处理领域的含义,特征抽取可以理解为:在尽可能多地保持相关信息的情况下,对数据进行压缩的一种方法。特征抽取通常用于提高计算效率,同样也可以帮助我们降低“维度灾难”——尤其当模型不适于正则化处理时。
主成分分析(principal component analysis,PCA)是一种广泛应用于不同领域的无监督线性数据转换技术,其突出作用是降维。PCA的其他常用领域包括:股票交易市场数据的探索性分析和信号去噪,以及生物信息学领域的基因组和基因表达水平数据分析等。PCA可以帮助我们基于特征之间的关系识别出数据内在的模式。简而言之,PCA的目标是在高维数据中找到最大方差的方向,并将数据映射到一个维度不大于原始数据的新的子空间上。如下图所示,以新特征的坐标是相互正交的为约束条件,新的子空间上正交的坐标轴(主成分)可被解释为方差最大的方向。在此,x1和x2为原始特征的坐标轴,而PC1和PC2即为主成分。

如果使用PCA降维,我们将构建一个d×k维的转换矩阵W,这样就可以将一个样本向量x映射到一个新的k维特征子空间上去,此空间的维度小于原始的d维特征空间:
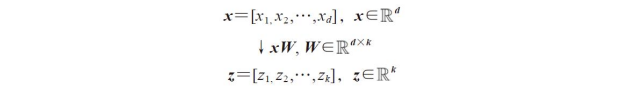
完成从原始d维数据到新的k维子空间(一般情况下k<<d)的转换后,第一主成分的方差应该是最大的,由于各主成分之间是不相关的(正交的),后续各主成分也具备尽可能大的方差。需注意的是,主成分的方向对数据值的范围高度敏感,如果特征的值使用不同的度量标准,我们需要先对特征进行标准化处理,以让各特征具有相同的重要性。
在详细讨论使用PCA算法降维之前,我们先通过以下几个步骤来概括一下算法的流程:
1)对原始d维数据集做标准化处理。
2)构造样本的协方差矩阵。
3)计算协方差矩阵的特征值和相应的特征向量。
4)选择与前k个最大特征值对应的特征向量,其中k为新特征空间的维度(k≤d)。
5)通过前k个特征向量构建映射矩阵W。
6)通过映射矩阵W将d维的输入数据集X转换到新的k维特征子空间。
5.1.1 总体方差与贡献方差
在本小节中,我们将学习主成分分析算法的前四个步骤:数据标准化、构造协方差矩阵、获得协方差矩阵的特征值和特征向量,以及按降序排列特征值所对应的特征向量:
首先,我们加载第4章已经使用过的葡萄酒数据集:

接下来,我们将葡萄酒数据集划分为训练集和测试集——分别占数据集的70%和30%,并使用单位方差将其标准化。

![]()
通过上述代码完成数据的预处理后,我们进入第二步:构造协方差矩阵。此d×d维协方差矩阵是沿主对角线对称的,其中d为数据集的维度,此矩阵成对地存储了不同特征之间的协方差。例如,对群体进行描述的两个特征xj和xk可通过如下公式计算它们之间的协方差:
![]()
在此,μj和μk分别为特征j和k的均值。请注意,如果我们对数据集做了标准化处理,样本的均值将为零。两个特征之间的协方差如果为正,说明它们会同时增减,而一个负的协方差值则表示两个特征会朝相反的方向变动。例如,一个包含三个特征的协方差矩阵可记为(注意:此处Σ代表希腊字母sigma,在此请勿与求和符号混为一谈):

协方差矩阵的特征向量代表主成分(最大方差方向),而对应的特征值大小就决定了特征向量的重要性。就葡萄酒数据集来说,我们可以得到13×13维协方差矩阵的13个特征向量及其对应的特征值。
现在,我们来计算协方差矩阵的特征对。通过线性代数或微积分的相关知识我们知道,特征值V需满足如下条件:
Σv=λv
此处的特征值是λ一个标量。由于手工计算特征向量和特征值从某种程度上来说是一项烦琐且复杂的工作,我们将使用NumPy中的linalg.eig函数来计算葡萄酒数据集协方差矩阵的特征对:

应用numpy.cov函数,我们计算得到了经标准化处理的训练数据集的协方差矩阵。使用linalg.eig函数,通过特征分解,得到一个包含13个特征值的向量(eigen_vals)及其对应的特征值,特征向量以列的方式存储于一个13×13维的矩阵中(eigen_vecs)。
因为要将数据集压缩到一个新的特征子空间上来实现数据降维,所以我们只选择那些包含最多信息(方差最大)的特征向量(主成分)组成子集。由于特征值的大小决定了特征向量的重要性,因此需要将特征值按降序排列,我们感兴趣的是排序在前k个的特征值所对应的特征向量。在整理包含信息量最大的前k个特征向量前,我们先绘制特征值的方差贡献率(variance explained ratios)图像。
特征值λj的方差贡献率是指,特征值λj与所有特征值和的比值:

使用NumPy的cumsum函数,我们可以计算出累计方差,其图像可通过matplotlib的step函数绘制:

由下图可以看到,第一主成分占方差总和的40%左右;此外,还可以看出前两个主成分占总体方差的近60%:
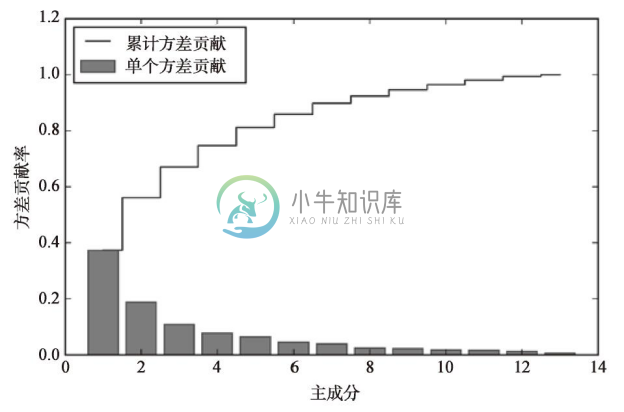
虽然方差贡献率图像可以让我们联想到第4章中通过随机森林计算出的关于特征的重要程度,但我们应注意:PCA是一种无监督方法,这意味着我们可以忽略类标信息。相对而言,随机森林通过类标信息来计算节点的不纯度,而方差度量的是特征值在轴线上的分布。
5.1.2 特征转换
在将协方差矩阵分解为特征对后,我们继续执行PCA方法的最后三个步骤,将葡萄酒数据集中的信息转换到新的主成分轴上。在本小节中,我们将对特征值按降序进行排列,并通过挑选出对应的特征向量构造出映射矩阵,然后使用映射矩阵将数据转换到低维的子空间上。
首先,按特征值的降序排列特征对:

接下来,我们选取两个对应的特征值最大的特征向量,这两个值之和占据了数据集总体方差的60%。请注意,出于演示的需要,我们只选择了两个特征向量,因为在本小节中我们将以二维散点图的方式绘制相关图像。在实际应用中,确定主成分的数量时,我们需要根据实际情况在计算效率与分类器性能之间做出权衡。

执行上述代码,通过选取的两个特征向量我们得到了一个13×2维的映射矩阵W。通过映射矩阵,我们可以将一个样本x(以13维的行向量表示)转换到PCA的子空间上得到x',样本转换为一个包含两个新特征的二维向量。
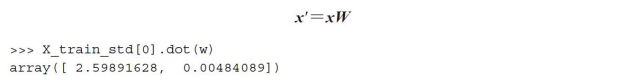
类似地,通过计算矩阵的点积,我们可以将整个124×13维的训练数据集转换到包含两个主成分的子空间上:

最后,转换后的葡萄酒数据集将以124×2维矩阵的方式存储,我们以二维散点图的方式来对其进行可视化展示:

![]()
在下图中可以看到,相较于第二主成分(y轴),数据更多地沿着x轴(第一主成分)方向分布,这与我们在上一小节中绘制的方差贡献率图是一致的。而且,可以直观地看到,线性分类器能够很好地对其进行划分:

为了演示散点图,我们使用了类标信息,但请注意PCA是无监督方法,无需类标信息。
5.1.3 使用scikit-learn进行主成分分析
通过上一小节中详尽的介绍,我们了解了PCA内部的工作原理,接下来讨论如何使用scikit-learn中提供的PCA类。PCA也是scikit-learn中的一个数据转换类,在使用相同的模型参数对训练数据和测试数据进行转换之前,我们首先要使用训练数据对模型进行拟合。下面,我们使用scikit-learn中的PCA对葡萄酒数据集做预处理,然后使用逻辑斯谛回归对转换后的数据进行分类,最后用第2章中定义的plot_decision_region函数对决策区域进行可视化展示。


执行上述代码后,我们可以看到将训练数据转换到两个主成分轴后生成的决策区域。

如果比较scikit-learn中提供的PCA类与我们自己实现的PCA类的分析结果,可以发现:上图可以看作是我们此前自己完成PCA方法所得到沿y轴进行旋转后的结果。出现此差异的原因,不是两种方法在实现中出现了什么错误,而在于特征分析方法:特征向量可以为正或者为负。这不是重点,因为有需要时我们可以在数据上乘以-1来实现图像的镜像。注意:特征向量通常会缩放到单位长度1。为了保证整个分析过程的完整性,我们绘制一下逻辑斯谛回归在转换后的测试数据上所得到的决策区域,看其是否能很好地将各类分开:

执行上述代码,我们绘制出了测试集的决策区域,可以看到:逻辑斯谛回归在这个小的二维特征子空间上表现优异,只误判了一个样本。

如果我们对不同主成分的方差贡献率感兴趣,可以将PCA类中的n_componets参数设置为None,由此,可以保留所有的主成分,并且可以通过explained_variance_ratio_属性得到相应的方差贡献率:

请注意:在初始化PCA类时,如果我们将n_components设置为None,那么它将按照方差贡献率递减顺序返回所有的主成分,而不是进行降维操作。

