3.4 使用支持向量机最大化分类间隔

另一种性能强大且广泛应用的学习算法是支持向量机（support vector machine，SVM），它可以看作对感知器的扩展。在感知器算法中，我们可以最小化分类误差。而在SVM中，我们的优化目标是最大化分类间隔。此处间隔是指两个分离的超平面（决策边界）间的距离，而最靠近超平面的训练样本称作支持向量（support vector），如下图所示：

3.4.1　对分类间隔最大化的直观认识

决策边界间具有较大的间隔意味着模型具有较小的泛化误差，而较小的间隔则意味着模型可能过拟合。为了对间隔最大化有个直观的认识，我们仔细观察一下两条平行的决策边界，我们分别称其为正、负超平面，可表示为：

如果我们将等式（1）（2）相减，可以得到：

我们可以通过向量w的长度来对其进行规范化，做如下定义：

由此可以得到如下等式：

上述等式的左侧可以解释为正、负超平面间的距离，也就是我们要最大化的间隔。

在样本正确划分的前提下，最大化分类间隔也就是使最大化，这也是SVM的目标函数，记为：

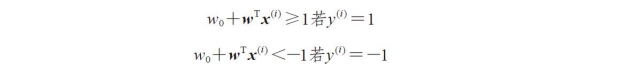
这两个方程可以解释为：所有的负样本都落在负超平面一侧，而所有的正样本则在正超平面划分出的区域中。它们可以写成更紧凑的形式：

在实践中，通过二次规划的方法，很容易对目标函数的倒数项进行最小化处理。不过关于二次规化的详细内容超出了本书的范围，如果读者感兴趣，可以通过阅读由Springer出版社出版，Vladimir Vapnik的The Nature of Statistical Learning Theory一书，或者查阅Chris J.C.Burger在其论文“A Tutorial on Support Vector Machines for Pattern Recognition”（发表于Data mining and knowledge discovery，2（2）:121～167，1998）中的精彩解释。

3.4.2　使用松弛变量解决非线性可分问题

我们无需对间隔分类背后的数学概念进行更深入的探讨，在此只是简单介绍一下松弛变量ξ的概念。它由Vladimir Vapnik在1995年引入，并由此提出所谓的软间隔分类。介绍松弛系数ξ的目的是：对于非线性可分的数据来说，需要放松线性约束条件，以保证在适当的罚项成本下，对错误分类的情况进行优化时能够收敛。

取值为正的松弛变量可以简单地加入到线性约束中：

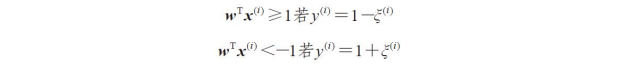
由此，在前面提及的约束条件下，新的优化目标为最小化下式：

通过变量C，我们可以控制对错误分类的惩罚程度。C值较大时，对应大的错误惩罚，当选择小的C值时，则对错误分类的惩罚没那么严格。因此，可以使用参数C来控制间隔的大小，进而可以在偏差和方差之间取得平衡，如下图所示：

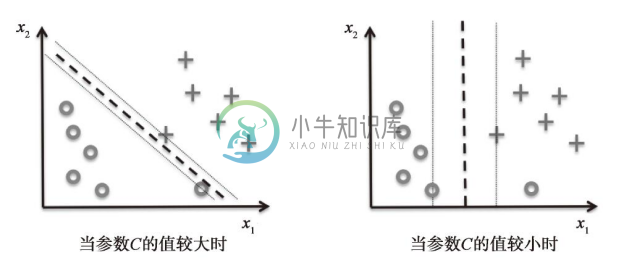
前面在回归的正则化中已经做了讨论，我们通过增加C的值来增加偏差并降低模型的方差。

至此，我们已经学习了线性SVM的基本概念，现在让我们来训练一个SVM模型以对鸢尾花数据集中的样本进行分类。

执行上述代码可以对通过SVM获得的决策区域进行可视化，结果如下图所示：

逻辑斯谛回归与支持向量机

在实际分类任务中，线性逻辑斯谛回归与支持向量机往往能得到非常相似的结果。逻辑斯谛回归会尽量最大化训练数据集的条件似然，这使得它比支持向量机更易于处理离群点。而支持向量机则更关注接近决策边界（支持向量）的点。逻辑斯谛回归的另一个优势在于模型简单从而更容易实现。此外，逻辑斯谛回归模型更新方便，当应用于流数据分析时，这是非常具备吸引力的。

3.4.3　使用scikit-learn实现SVM

前面章节中用到了scikit-learn中的Perceptron和LogisticRegression类，它们都使用了LIBLINEAR库，LIBLINEAR是一个由中国台湾大学（http://www.csie.ntu.edu.tw/~cjlin/liblinear/）使用C/C++语言开发的经过高度优化的库。类似地，用于训练SVM模型的SVC类使用了LIBSVM库，它是一个专门用于SVM的C/C++库（http://www.csie.ntu.edu.tw/~cjlin/libsvm/）。

与使用原生Python代码实现线性分类器相比，使用LIBLINEAR和LIBSVM库实现有其优点：在用于大型数据时，可以获得极高的训练速度。然而，有些时候数据集非常巨大以致无法加载到内存中，针对这种情况，scikit-learn提供了SGDClassifier类供用户选择，这个类还通过partial_fit方法支持在线学习。SGDClassifier类背后的概念类似于第2章中实现的随机梯度算法。我们可以使用默认参数以如下方式分别初始化基于随机梯度下降的感知器、逻辑斯谛回归以及支持向量机模型。