12.3 人工神经网络的训练

优质

小牛编辑

129浏览

2023-12-01

我们已经了解了神经网络在的具体应用，并通过学习代码对其如何工作有了基本的认识，现在我们将更深入挖掘一些概念，如用于权值学习的逻辑斯谛代价函数（logistic cost function）和反向传播（backpropagation）算法。

12.3.1　计算逻辑斯谛代价函数

我们在_get_cost方法中实现的逻辑斯谛代价函数其实很简单，它实际上与我们在第3章逻辑斯谛回归那一小节中介绍的代价函数完全一致。

其中，a^（i）是前向传播过程中，用来计算某层中第i个单元的sigmoid激励函数。

现在，我们加入一个正则化项，它可以帮助我们降低过拟合的程度。回忆一下前面章节中的内容，L2和L1正则化项定义如下（请记住，我们不对偏置单元进行正则化处理）：

虽然L1和L2正则化均适用于我们的多层感知器模型，为简单起见，我们只关注L2正则化项。不过这些同样的概念也适用于L1正则化项。通过在逻辑斯谛代价函数中加入L2正则化项，我们可得到如下公式：

我们已经实现了一个用于多类别分类的多层感知器，它返回一个包含t个元素的输出向量，我们需要将其与使用独热编码表示的t×1维目标向量进行比较。例如，对于一个特定的样本来说，它在第三层的激励和目标类别（此处为类别2）可能如下所示：

由此，我们需要将逻辑斯谛代价函数运用到网络中的所有激励单元j。因此我们的代价函数（未加入正则化项）变为：

其中，上标i为训练集中特定样本的索引。

下面经泛化的正则化项看起来有点复杂，不过在此我们仅计算l层所有加到第一列权重的总和（不包含偏置项）

以下公式表示L2罚项：

请记住，我们的目标是最小化代价函数J（w）。因此，须计算矩阵W对网络各层中每个权重的偏导：

在下一节中，我们将讨论反向传播算法，它能够通过计算偏导最小化代价函数。

请注意，W包含多个矩阵。在仅包含一个隐层单元的多层感知器中，可通过权重矩阵W^（1）将输入层与隐层相连，而W^（2）则连接隐层与输出层。下图以一种直观的方式对矩阵W进行可视化展示：

在这个简化图中，矩阵W^（1）和W^（2）均具有相同的行数和列数，此情况仅当多层感知器的隐层、输入层、输出层数量相同时才会出现。

如果对此感到困惑，请进入下一节，我们将通过反向传播算法详细讨论W^（1）和W^（2）维度方面的内容。

12.3.2　通过反向传播训练神经网络

在本节中，我们将通过讲解反向传播算法中相关数学公式，使读者理解神经网络是如何通过学习高效获得权重的。每个人对数学表示方法的熟练程度不同，因此下面将要介绍的公式可能看起来会有些复杂。许多人喜欢自底向上的方法，通过公式的逐步讲解形成对算法的直观认识。不过，如果你喜欢自顶向下的方法，并且希望在不使用数学符号的情况下了解反向传播算法，建议读者先阅读下一节内容后再来学习本节内容。

在上一节中，我们学习了如何通过最后一层的激励以及目标类标之间的差异来计算代价。现在，我们将了解一下反向传播算法如何更新多层感知器模型的权重，_get_gradient方法已实现了该算法。回忆下本章开始时介绍的内容，我们首先需要通过正向传播来获得输出层的激励，可将其形式化为：

简单地说，我们只是按照下图所示，通过网络中的连接将输入向前传递：

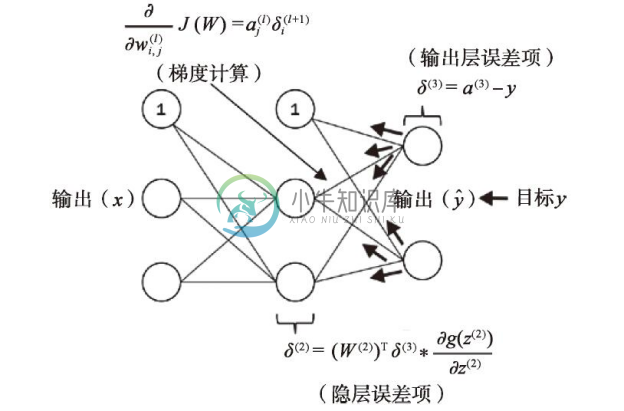
在反向传播中，错误被从右至左传递。我们首先计算输出层的误差向量：

其中，y为真实类标的向量。

接下来，我们计算隐层的误差项：

请注意：星号（*）在此表示逐元素相乘。

虽然无需太过在意下面的公式，不过读者可能会好奇：激励函数的导数是如何得到的？在此逐步演示求导过程：

为了更好地理解δ^（2）项的计算，我们对此进行更详细的讨论。在前面的公式中，我们将其与t×h维矩阵W^（2）的转置（W^（2））^T相乘，t为输出类标的数量，而h为隐层单元的数量。现在，（W^（2））^T与t×1维向量δ^（2）的乘积为h×t维矩阵。我们将（W^（2））^Tδ^（3）与（a^（2）*（1-a^（2）））逐项相乘，结果也是一个t×1维的向量。最后，在得到δ后，我们可将代价函数的导数写作：