4.4 将特征的值缩放到相同的区间

特征缩放（peature scaling）是数据预处理过程中至关重要的一步，但却极易被人们忽略。决策树和随机森林是机器学习算法中为数不多的不需要进行特征缩放的算法。然而，对大多数机器学习和优化算法而言，将特征的值缩放到相同的区间可以使其性能更佳，例如在第2章实现的梯度下降（gradient descent）优化算法。

特征缩放的重要性可以通过一个简单的例子来描述。假定我们有两个特征：一个特征值的范围为1～10；另一个特征值的范围为1～100000。回忆一下第2章中Adaline的平方误差函数，直观地说，算法将主要根据第二个特征上较大的误差进行权重的优化。另外还有k-近邻（k-nearest neighbor，KNN）算法，它以欧几里得距离作为相似性度量，样本间距离的计算也以第二个特征为主。

目前，将不同的特征缩放到相同的区间有两个常用的方法：归一化（normalization）和标准化（standardization）。这两个词在不同的领域中使用较为宽松，其含义由具体语境所确定。多数情况下，归一化指的是将特征的值缩放到区间[0,1]，它是最小-最大缩放的一个特例。为了对数据进行规范化处理，我们可以简单地在每个特征列上使用min-max缩放，通过如下公式可以计算出一个新的样本x^（i）的值：

其中，x^（i）是一个特定的样本，x_min和x_max分别是某特征列的最小值和最大值。

在scikit-learn中，已经实现了最小-最大缩放，使用方法如下：

当遇到需将数值限定在一个有界区间的情况时，我们常采用最小-最大缩放来进行有效的规范化。但在大部分机器学习算法中，标准化的方法却更加实用。这是因为：许多线性模型，如第3章中讨论过的逻辑斯谛回归和支持向量机，在对它们进行训练的最初阶段，即权重初始化阶段，可将其值设定0或是趋近于0的随机极小值。通过标准化，我们可以将特征列的均值设为0，方差为1，使得特征列的值呈标准正态分布，这更易于权重的更新。此外，与最小-最大缩放将值限定在一个有限的区间不同，标准化方法保持了异常值所蕴含的有用信息，并且使得算法受到这些值的影响较小。

标准化的过程可用如下方程表示：

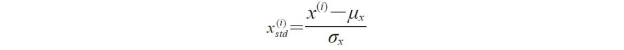
其中，μ_x和σ_x分别为样本某个特征列的均值和标准差。

在包含值为0～5的数据样本上，采用标准化和归一化两种常用的技术进行特征缩放，其两者之间的区别如下表所示：

与MinMaxScaler类似，scikit-learn也已经实现了标准化类：

需要再次强调的是：我们只是使用了StandardScaler对训练数据进行拟合，并使用相同的拟合参数来完成对测试集以及未知数据的转换。