10.6 回归中的正则化方法

正如第3章中所讨论的，正则化是通过在模型中加入额外信息来解决过拟合问题的一种方法，引入罚项增加了模型的复杂性但却降低了模型参数的影响。最常见的正则化线性回归方法就是所谓的岭回归（Ridge Regression）、最小绝对收缩及算子选择（Least Absolute Shrinkage and Selection Operator，LASSO）以及弹性网络（Elastic Net）等。

岭回归是基于L2罚项的模型，我们只是在最小二乘代价函数中加入了权重的平方和：

其中：

通过增加超参的值，我们可以增加正则化的强度，同时也就降低了权重对模型的影响。请注意，正则化项不影响截距项w₀。

对于基于稀疏数据训练的模型，还有另外一种解决方案，即LASSO。基于正则化项的强度，某些权重可以变为零，这也使得LASSO成为一种监督特征选择技术：

其中：

不过LASSO存在一个限制，即如果m＞n，则至多可以完成n个变量的筛选。弹性网络则是岭回归和LASSO之间的一个折中，其中包含一个用于稀疏化的L1罚项，以及一个消除LASSO限制（如可筛选变量数量）的L2罚项。

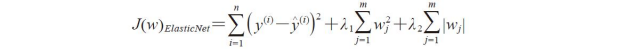
scikit-learn中包含前面提及的所有正则化回归模型，除了需要参数指定正则化强度外，这些模型的使用方式与k折交叉验证等普通回归模型的使用方法相同。

岭回归模型的初始化方式如下：

请注意，正则化强度通过alpha来调节，它类似于参数。同样，我们可以使用linear_model子模块下的Lasso对象来初始化LASSO回归：

最后，scikit-learn下的ElasticNet允许我们调整L1与L2的比率：

例如，如果将l1_ratio设置为1.0，此时ElasticNet回归等同于LASSO回归。如想了解线性回归不同实现方式的更多信息请参见：http://scikit-learn.org/stable/modules/linear_model.html。