5.3 使用核主成分分析进行非线性映射

优质

小牛编辑

124浏览

2023-12-01

许多机器学习算法都假定输入数据是线性可分的。感知器为了保证其收敛性，甚至要求训练数据是完美线性可分的。我们目前学习过的算法中，像Adaline、逻辑斯谛回归和（标准）支持向量机等，都将无法实现完美线性划分的原因归咎于噪声。然而，在现实世界中，大多数情况下我们面对的是非线性问题，针对此类问题，通过降维技术，如PCA和LDA等，将其转化为线性问题并不是最好的方法。在本小节中，我们将了解一下利用核技巧的PCA，或者称为核PCA，这与在第3章中我们介绍过的核支持向量机的概念有一定相关性。使用核PCA，我们将学习如何将非线性可分的数据转换到一个适合对其进行线性分类的新的低维子空间上。

5.3.1　核函数与核技巧

回忆一下我们在第3章中曾讨论过的基于核的支持向量机，通过将非线性可分问题映射到维度更高的特征空间，使其在新的特征空间上线性可分。为了将样本x∈R^d转换到维度更高的k维子空间，我们定义如下非线性映射函数φ：

我们可以将φ看作是一个函数，它能够对原始特征进行非线性组合，以将原始的d维数据集映射到更高维的k维特征空间。例如：对于二维（d＝2）特征向量x∈R^d（x是包含d个特征的列向量）来说，可用如下映射将其转换到三维空间：

换句话说，利用核PCA，我们可以通过非线性映射将数据转换到一个高维空间，然后在此高维空间中使用标准PCA将其映射到另外一个低维空间中，并通过线性分类器对样本进行划分（前提条件是，样本可根据输入空间的密度进行划分）。但是，这种方法的缺点是会带来高昂的计算成本，这也正是我们为什么要使用核技巧的原因。通过使用核技巧，我们可以在原始特征空间中计算两个高维特征空间中向量的相似度。

在更深入了解使用核技巧解决计算成本高昂的问题之前，我们先回顾一下本章最初所介绍的标准PCA方法。两个特征k和j之间协方差的计算公式如下：

由于在对特征做标准化处理后，其均值为0，例如：我们可将上述公式简化为：

请注意，上述公式是两个特征值之间的协方差计算公式，下面给出计算协方差矩阵Σ的通用公式：

Bernhard Schoellkopf提出了一种方法^[1]，可以使用φ通过在原始特征空间上的非线性特征组合来替代样本间点积的计算：

为了求得此协方差矩阵的特征向量，也就是主成分，我们需要求解下述公式：

其中，λ和v分别为协方差矩阵Σ的特征值和特征向量，这里的a可以通过提取核（相似）矩阵K的特征向量来得到，具体内容在将后续段落中进行介绍。

核矩阵的推导过程如下：

首先，使用矩阵符号来表示协方差矩阵，其中φ（X）是一个n×k维的矩阵：

现在，我们可以将特征向量的公式记为：

由于Σv＝λv，我们可以得到：

两边同乘以φ（X），可得：

其中，K为相似（核）矩阵：

回顾一下3.4节的内容，通过核技巧，使用核函数K以避免使用φ来精确计算样本集合x中样本对之间的点积，这样我们就无需对特征向量进行精确的计算：

换句话说，通过核PCA，我们能够得到已经映射到各成分的样本，而不像标准PCA方法那样去构建一个转换矩阵。简单地说，可以将核函数（或者简称为核）理解为：通过两个向量点积来度量向量间相似度的函数。最常用的核函数有：

·多项式核：

其中，阈值θ和幂的值p需自行定义。

·双曲正切（sigmoid）核：

·径向基核函数（Radial Basis Function，RBF）或者称为高斯核函数，我们将在下一小节的示例中用到：

也可以写作：

综合上述讨论，我们可以通过如下三个步骤来实现一个基于RBF核的PCA：

1）为了计算核（相似）矩阵k，我们需要做如下计算：

我们需要计算任意两样本对之间的值：

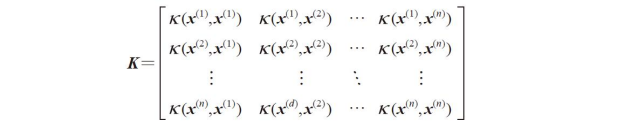
例如：如果数据集包含100个训练样本，将得到一个100×100维的对称核矩阵。

2）通过如下公式进行计算，使核矩阵k更为聚集：

3）将聚集后的核矩阵的特征值按照降序排列，选择前k个特征值所对应的特征向量。与标准PCA不同，这里的特征向量不是主成分轴，而是将样本映射到这些轴上。

至此，读者可能会感到困惑：为什么要在第2步中对核矩阵进行聚集处理？我们曾经假定，数据需要经过标准化处理，当在生成协方差矩阵并通过φ以非线性特征的组合替代点积时，所有特征的均值为0。由此，在第2步中聚集核矩阵就显得很有必要，因为我们并没有精确计算新的特征空间，而且也不能确定新特征空间的中心在零点。

下一小节中，我们将基于这三个步骤使用Python实现核PCA。

[1] B. Scholkopf, A. Smola, and K.-R. Muller. Kernel Principal Component Analysis. pages 583–588, 1997.

5.3.2　使用Python实现核主成分分析

在前面的小节中，我们讨论了核PCA相关的核心概念。现在根据之前总结过的实现核PCA方法的三个步骤，使用Python实现基于RBF核的PCA。借助于SciPy和NumPy的函数，我们将会看到，实现核PCA实际上很简单。

采用RBF核函数实现的PCA进行降维时存在一个问题，就是我们必须指定先验参数r需要通过实验来找到一个合适的r值，最好是通过参数调优算法来确定，例如网格搜索法，我们将在第6章中对其进行深入探讨。

1.示例一：分离半月形数据

现在，我们将实现的rbf_kernel_pca方法应用于非线性示例数据集。我们首先创建一个包含100个样本点的二维数据集，以两个半月形状表示：

出于演示的需要，使用三角符号标识的表示一个类别中的样本，使用圆形符号标识的表示另一类别的样本：

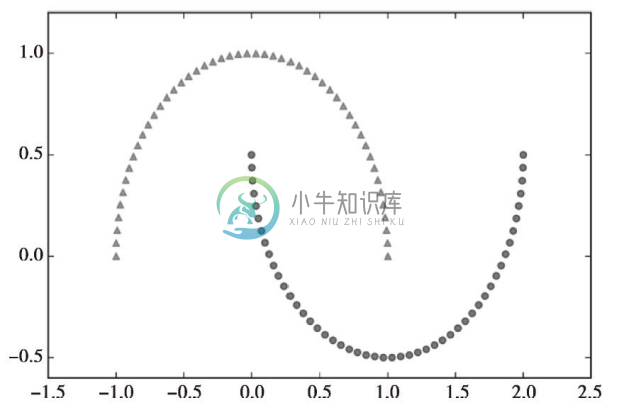
显然，这两个半月形不是线性可分的，而我们的目标是通过核PCA将这两个半月形数据展开，使得数据集成为适用于某一线性分类器的输入数据。首先，我们通过标准的PCA将数据映射到主成分上，并观察其形状：

很明显，经过标准PCA的转换后，线性分类器未必能很好地发挥其作用：

请注意，当我们仅绘制第一主成分的图像时（见右子图），我们分别将三角形和圆形代表的样本向上或向下做了轻微调整，以更好地展示类间重叠。

请注意，PCA是无监督方法，与LDA相比，它在使得方差最大化的过程中未使用类标信息。出于增强可视化效果的考虑，为了显示分类的程度，我们才在此使用了三角形和圆形符号。

现在我们将使用前一小节中实现的核PCA函数：rbf_kernel_pca：

可以看到，两个类别（圆形和三角形）此时是线性可分的，这使得转换后的数据适合作为线性分类器的训练数据集：

不过，对于可调整参数γ，没有一个通用的值使其适用于不同的数据集。针对给定问题找到一个适宜的参数值需要通过实验来解决。在第6章中，我们将讨论可自动进行参数优化等任务的技术。这里，我使用了一个已有的能够生成良好结果的值。

2.示例二：分离同心圆

在上一小节，我们演示了如何通过核PCA分离半月形数据。既然我们已经投入了如此多的精力去理解核PCA的概念，就再看一下另外一个关于非线性问题的有趣例子——同心圆。

代码如下：

同样，我们假设了一个涉及两个类别的问题，三角形和圆形分别标识不同类别的样本：

首先使用标准PCA方法，以便将其结果与基于RBF核的PCA生成的结果进行比较：

再一次发现，通过标准PCA无法得到适合于线性分类器的训练数据：

给定一个合适的γ值，来看看基于RBF的核PCA实现能否得到令人满意的结果：

基于RBF的核PCA再一次将数据映射到了一个新的子空间中，使两个类别变得线性可分：

5.3.3　映射新的数据点

在上述两个核PCA应用的例子（半月形和同心圆）中，我们都将单一数据集映射到一个新的特征上。但在实际应用中，我们可能需要转换多个数据集，例如，训练数据、测试数据，以及在完成模型构建和评估后所要收集的新样本。本节将介绍如何映射训练数据集以外的数据点。

在本章开始时介绍过的标准PCA方法中，我们通过转换矩阵和输入样本之间的点积来对数据进行映射；映射矩阵的列是协方差矩阵中k个最大特征值所对应的特征向量（v）。现在的问题是：如何将此概念应用于核PCA？回忆一下核PCA的原理可以记得，我们从聚集核矩阵（不是协方差矩阵）中得到了特征向量（a），这意味着样本已经映射到了主成分轴v。由此，如果我们希望将新的样本（x′）映射到此主成分轴，需要进行如下计算：