12.5 通过梯度检验调试神经网络

实现人工神经网络是相当复杂的，而手动检查已实现的反向传播算法是否正确向来被视作一个好的方法。在本节中，我们将讨论一个称作梯度检验（gradient checking）的简单过程，它本质上是网络解析梯度与数值梯度之间的比较。梯度检验并不只限定于前馈神经网络，它也适用于其他基于梯度优化的神经网络架构。即使读者要实现基于梯度优化的普通算法，如线性回归、逻辑斯谛回归，以及支持向量机等，使用梯度检验来验证一下梯度的计算是否正确也是一个不错的主意。

在上一节中，我们将代价函数定义为J（W），其中W为人工神经网络的权重系数矩阵。请注意：粗略来说，J（W）是包含一个隐层的多层感知器中W^（1）和W^（2）的堆叠。我们将W^（1）定义为h×[m+1]维的矩阵，通过它将输入层连接到隐层，其中h为隐层元素的数量，而m为特征（输入单元）的数量。而连接隐层与输出层的W^（2）矩阵维度为t×h，其中t为输出单元的数量。进而计算代价函数对于权重的导数：

请记住，我们沿着梯度相反的方向进行权重的更新。在梯度检验中，我们将此分析结果与一个数值近似梯度进行比较：

这里，ε通常是一个极小的数值，如1e-5（请注意这里1e-5仅是0.00001的更为简洁的记法）。直观上看，我们将此有限的近似差异看作是连接代价函数上两个权重w和w＋ε（二者均为标量）之间直线的斜率。为了简单起见，我们忽略了上下标：

得到一个更为准确的梯度近似值的方法是：计算两点间代价函数之差与对应两点间横坐标距离之商：

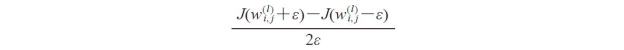
通常情况下，L2向量范数可以通过数值梯度与解析梯度之差来进行计算。在实践中，我们通常将经过计算的梯度矩阵展开为一个向量，这样可以更方便地计算误差（梯度向量之间的差异）：

这里有一个问题：随着尺度的变动，误差值并非不变（当权重向量范数很小的时候，即便很小的误差也会感觉很明显）。由此，对误差进行归一化处理：

现在，我们希望数值梯度与解析梯度之间的相对误差尽可能小。在实现梯度检验之前，我们还需仔细考虑一个问题：以多大的可接受误差作为通过梯度验证的阈值？通过梯度检验的相对误差阈值与网络架构的复杂性息息相关。一般来说，在正确实现反向传播算法的前提下，我们添加的隐层数量越多，数值梯度与解析梯度间的差异就越大。由于我们在本章中实现的神经网络比较简单，因此可以对阈值做一个相对严格的限制，规则如下：

·相对误差小于等于1e-7意味着一切正常！

·相对误差小于等于1e-4意味着条件可能存在问题，需要检查。

·相对误差大于1e-4意味着代码中可能存在某些错误。

我们已经建立好了基本规则，现在开始实现梯度检验。为了做到这一点，我们可以简单使用前面实现的NeuralNetMLP类，并在类中增加如下方法：

_gradient_checking方法中的代码看起来相当简单。我的个人建议就是尽量保持代码的简单易懂。我们的目的是仔细检查梯度计算，因此要保证在梯度检验中，不会因为代码高效却复杂，就带来额外错误。接下来，仅需对fit方法做稍许修改。出于清晰易读的考虑，下面的代码中省略了fit函数开始部分的代码，只需将注释##start gradient checking与##end gradient checking之间列出的代码加入到原来实现的fit方法中：

假定将更改后的多层感知器类命名为MLPGradientCheck，我们现在来初始化一个新的包含10个隐层的多层感知器。同时，我们禁用了正则化、自适应学习，以及动量学习。此外，通过将minibatches的值设置为1来使用常规梯度下降算法。代码如下：

梯度检验的一个缺点就是，它的计算成本极其昂贵。引入梯度检验会使神经网络的训练过程变得非常缓慢，因此我们只希望在算法调试时才用到它。基于此原因，仅使用少量训练样本进行梯度检验屡见不鲜（在此，我们使用了5个样本）。代码如下：

从代码的输出结果来看，我们的多层感知器完美通过了测试。