深度神经网络实践

优质

小牛编辑

131浏览

2023-12-01

代码见nn_overfit.py

优化

Regularization

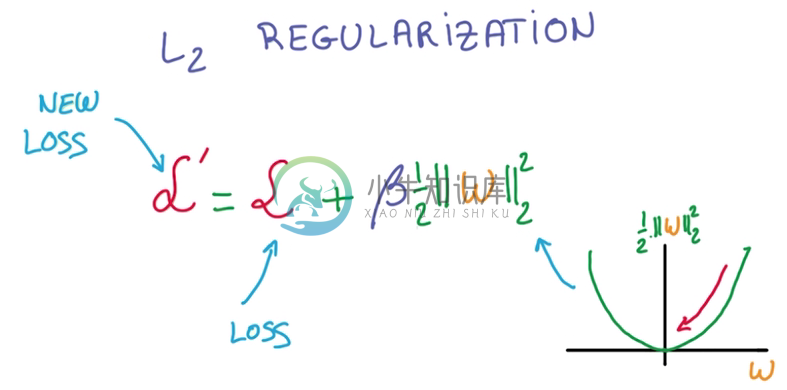
在前面实现的RELU连接的两层神经网络中，加Regularization进行约束，采用加l2 norm的方法，进行负反馈：

代码实现上，只需要对tf_sgd_relu_nn中train_loss做修改即可：

可以用tf.nn.l2_loss(t)对一个Tensor对象求l2 norm
需要对我们使用的各个W都做这样的计算（参考tensorflow官方example）

l2_loss = tf.nn.l2_loss(weights1) + tf.nn.l2_loss(weights2)

添加到train_loss上
这里还有一个重要的点，Hyper Parameter: β
- 我觉得这是一个拍脑袋参数，取什么值都行，但效果会不同，我这里解释一下我取β=0.001的理由
- 如果直接将l2_loss加到train_loss上，每次的train_loss都特别大，几乎只取决于l2_loss
- 为了让原本的train_loss与l2_loss都能较好地对参数调整方向起作用，它们应当至少在同一个量级
- 观察不加l2_loss，step 0 时，train_loss在300左右
- 加l2_loss后， step 0 时，train_loss在300000左右
- 因此给l2_loss乘0.0001使之降到同一个量级
```
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=tf_train_labels)) + 0.001 * l2_loss
```
- 所有其他参数不变，训练3000次，准确率提高到92.7%
- 黑魔法之所以为黑魔法就在于，这个参数可以很容易地影响准确率，如果β = 0.002，准确率提高到93.5%

OverFit问题

在训练数据很少的时候，会出现训练结果准确率高，但测试结果准确率低的情况

缩小训练数据范围：将把batch数据的起点offset的可选范围变小（只能选择0-1128之间的数据）：

offset_range = 1000
offset = (step * batch_size) % offset_range

可以看到，在step500后，训练集就一直是100%，验证集一直是77.6%，准确度无法随训练次数上升，最后的测试准确度是85.4%

DropOut

采取Dropout方式强迫神经网络学习更多知识

参考aymericdamien/TensorFlow-Examples中dropout的使用

我们需要丢掉RELU出来的部分结果
调用tf.nn.dropout达到我们的目的：

keep_prob = tf.placeholder(tf.float32)
if drop_out:
    hidden_drop = tf.nn.dropout(hidden, keep_prob)
    h_fc = hidden_drop

这里的keep_prob是保留概率，即我们要保留的RELU的结果所占比例，tensorflow建议的语法是，让它作为一个placeholder，在run时传入
当然我们也可以不用placeholder，直接传一个0.5：

if drop_out:
    hidden_drop = tf.nn.dropout(hidden, 0.5)
    h_fc = hidden_drop

这种训练的结果就是，虽然在step 500对训练集预测没能达到100%（起步慢），但训练集预测率达到100%后，验证集的预测正确率仍然在上升
这就是Dropout的好处，每次丢掉随机的数据，让神经网络每次都学习到更多，但也需要知道，这种方式只在我们有的训练数据比较少时很有效
最后预测准确率为88.0%

Learning Rate Decay

随着训练次数增加，自动调整步长

在之前单纯两层神经网络基础上，添加Learning Rate Decay算法
使用tf.train.exponential_decay方法，指数下降调整步长，具体使用方法官方文档说的特别清楚
注意这里面的cur_step传给优化器，优化器在训练中对其做自增计数
与之前单纯两层神经网络对比，准确率直接提高到90.6%

Deep Network

增加神经网络层数，增加训练次数到20000

为了避免修改网络层数需要重写代码，用循环实现中间层

# middle layer
for i in range(layer_cnt - 2):
     y1 = tf.matmul(hidden_drop, weights[i]) + biases[i]
     hidden_drop = tf.nn.relu(y1)
     if drop_out:
         keep_prob += 0.5 * i / (layer_cnt + 1)
         hidden_drop = tf.nn.dropout(hidden_drop, keep_prob)

初始化weight在迭代中使用

for i in range(layer_cnt - 2):
     if hidden_cur_cnt > 2:
         hidden_next_cnt = int(hidden_cur_cnt / 2)
     else:
         hidden_next_cnt = 2
     hidden_stddev = np.sqrt(2.0 / hidden_cur_cnt)
     weights.append(tf.Variable(tf.truncated_normal([hidden_cur_cnt, hidden_next_cnt], stddev=hidden_stddev)))
     biases.append(tf.Variable(tf.zeros([hidden_next_cnt])))
     hidden_cur_cnt = hidden_next_cnt

第一次测试时，用正太分布设置所有W的数值，将标准差设置为1，由于网络增加了一层，寻找step调整方向时具有更大的不确定性，很容易导致loss变得很大
因此需要用stddev调整其标准差到一个较小的范围（怎么调整有许多研究，这里直接找了一个来用）

stddev = np.sqrt(2.0 / n)

启用regular时，也要适当调一下β，不要让它对原本的loss造成过大的影响
DropOut时，因为后面的layer得到的信息越重要，需要动态调整丢弃的比例，到后面的layer，丢弃的比例要减小

keep_prob += 0.5 * i / (layer_cnt + 1)

训练时，调节参数，你可能遇到消失的梯度问题，对于一个幅度为1的信号，在BP反向传播梯度时，每隔一层下降0.25，指数下降使得后面的层级根本接收不到有效的训练信号
官方教程表示最好的训练结果是，准确率97.5%，
我的nn_overfit.py开启六层神经网络，启用Regularization、DropOut、Learning Rate Decay，训练次数20000（应该还有再训练的希望，在这里虽然loss下降很慢了，但仍然在下降），训练结果是，准确率95.2%