10.2 波士顿房屋数据集
在实现第一个线性回归模型之前，先介绍一个新的数据集：波士顿房屋数据集（Housing Dataset），它是由D.Harrison和D.L.Rubinfeld于1978年收集的波士顿郊区房屋的信息。此房屋数据集可免费使用，读者可在UCI机器学习数据库中下载：https://archive.ics.uci.edu/ml/datasets/Housing。
数据集中506个样本的特征描述如下：
·CRIM：房屋所在镇的犯罪率。
·ZN：用地面积远大于25000平方英尺[1]的住宅所占比例。
·INDUS：房屋所在镇无零售业务区域所占比例。
·CHAS：与查尔斯河有关的虚拟变量（如果房屋位于河边则值为1，否则为0）。
·NOX：一氧化氮浓度（每千万分之一）。
·RM：每处寓所的平均房间数。
·AGE：业主自住房屋中，建于1940年之前的房屋所占比例。
·DIS：房屋距离波士顿五大就业中心的加权距离。
·RAD：距离房屋最近公路入口编号。
·TAX：每一万美元全额财产税金额。
·PTRATIO：房屋所在镇的师生比。
·B：计算公式为1000（Bk－0.63）^2，其中Bk为房屋所在镇非裔美籍人口所占比例。
·LSTAT：弱势群体人口所占比例。
·MEDV：业主自住房屋的平均价格（以1000美元为单位）。
在本章的后续内容中，我们将以房屋价格（MEDV）作为目标变量——使用其他13个变量中的一个或多个值作为解释变量对其进行预测。在进一步研究此数据集之前，我们先从UCI库中把它导入到pandas的DataFrame中：
为了确保数据已经正确加载，我们先显示数据集的前5行，如下图所示：
可视化数据集的重要特征
探索性数据分析（Exploratory Data Analysis，EDA）是机器学习模型训练之前的一个重要步骤。在本节的后续内容中，借助EDA图形工具箱中那些简单且有效的技术，可以帮助我们直观地发现数据中的异常情况、数据的分布情况，以及特征间的相互关系。
首先，借助散点图矩阵，我们以可视化的方法汇总显示各不同特征两两之间的关系。为了绘制散点图矩阵，我们需要用到seaborn库中的pairplot函数（http://stanford.edu/~mwaskom/software/seaborn/），它是在matplotlib基础上绘制统计图像的Python库。
如下图所示，散点图矩阵以图形的方式对数据集中特征间关系进行了描述：
导入seaborn库后，会覆盖当前Python会话中matplotlib默认的图像显示方式。如果读者不希望使用seaborn风格的设置，可以通过如下命令重设为matplotlib的风格：
出于篇幅限制及可读性的考虑，我们仅绘制了数据集中的5列：LSTAT、INDUS、NOX、RM和MEDV。不过，建议读者绘制整个DataFrame的散点图矩阵，以对数据做进一步的探索。
通过此散点图矩阵，我们可以快速了解数据是如何分布的，以及其中是否包含异常值。例如，我们可直观看出RM和房屋价格MEDV（第5列和第4行）之间存在线性关系。此外，从MEDV直方图（散点图矩阵的右下角子图）中可以发现：MEDV看似呈正态分布，但包含几个异常值。
请注意，不同于人们通常的理解，训练一个线性回归模型并不需要解释数量或者目标变量呈正态分布。正态假设仅适用于某些统计检验和假设检验（Montgomery,D.C.,Peck,E.A.,and Vining,G.G.Introduction to linear regression analysis.John Wiley and Sons,2012,pp.318-319），这些内容已经超出了本书讲解的范围，有兴趣的读者可以根据自身情况进行学习。
为了量化特征之间的关系，我们创建一个相关系数矩阵。相关系数矩阵与我们第5章“主成分分析”一节中讨论过的协方差矩阵是密切相关的。直观上来看，我们可以把相关系数矩阵看作协方差矩阵的标准化版本。实际上，相关系数矩阵就是在将数据标准化后得到的协方差矩阵。
相关系数矩阵是一个包含皮尔逊积矩相关系数（Pearson product-moment correlation coefficient，通常记为Pearson抯r）的方阵，它用来衡量两两特征间的线性依赖关系。相关系数的取值范围为-1到1。如果r＝1，代表两个特征完全正相关；如果r＝0，则不存在相关关系；如果r＝-1，则两个特征完全负相关。如前所述，皮尔逊相关系数可用两个特征x和y间的协方差（分子）除以它们标准差的乘积（分母）来计算。
其中，μ为样本对应特征的均值，σxy为特征x和y间的协方差，而σx和σy分别为两个特征的标准差。
可以证明：经标准化各特征间的协方差实际上等价于它们的线性相关系数。
首先对特征x和y做标准化处理，得到它们的z分数（z-score），并分别记为x'和y'：
我们曾经使用下面的公式计算过两个特征（人口）间的协方差：
由于特征经标准化后，其均值为0，由此，可通过下式来计算特征经缩放后的协方差：
将x'和y'带入后，可得：
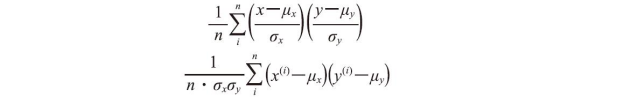
上式可简写为：
在下面的示例代码中，将使用NumPy的corrcoef函数计算前面散点图矩阵中5个特征间的相关系数矩阵，并使用seaborn的heatmap函数绘制其对应的热度图：
从结果图像中可见，相关系数矩阵为我们提供了另外一种有用的图形化数据描述方式，由此可以根据各特征间的线性相关性进行特征选择：
为了拟合线性回归模型，我们主要关注那些跟目标变量MEDV高度相关的特征。观察前面的相关系数矩阵，可以发现MEDV与变量LSTAT的相关性最大（-0.74）。大家应该还记得，前面的散点图矩阵显示LSTAT和MEDV之间存在明显的非线性关系。另一方面，正如散点图矩阵所示，RM和MEDV间的相关性也较高（0.70），考虑到从散点图中观察到了这两个变量之间的线性关系，因此，在后续小节，中使用RM作为解释变量进行简单线性回归模型训练，是一个较好的选择。
[1] 1平方英尺≈0.093平方米。