python Gabor滤波器讲解

解读Gabor滤波器

Fourier 变换是一种信号处理的有力工具，可以将图像从空域转换到频域，并提取到空域上不易提取到的特征。但是Fourier变换缺乏时间和位置的局部信息。
Gabor 变换是一种短时加窗Fourier变换（简单理解起来就是在特定时间窗内做Fourier变换），是短时傅里叶变换中窗函数取为高斯函数时的一种特殊情况。因此，Gabor滤波器可以在频域上不同尺度、不同方向上提取相关的特征。另外，Gabor函数与人眼的作用相仿，所以经常用作纹理识别上，并取得了较好的效果。
在二维空间中，使用一个三角函数(a)（如正弦函数）与一个高斯函数(b)叠加，我们得到了一个Gabor滤波器(c)。如下图所示：

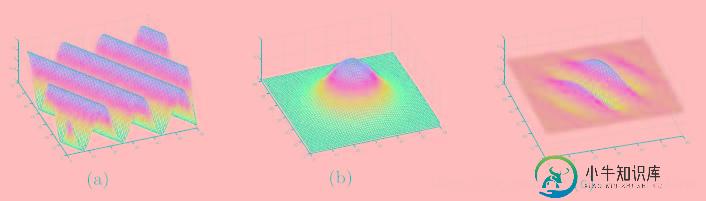
Gabor函数解读

二维Gabor函数的数学表达式如下：

复数表示：

实数部分：

虚数部分：

x'、y' 计算公式：

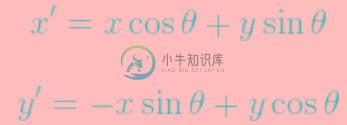
介绍公式中各个参数的含义：

波长(λ)：表示Gabor核函数中余弦函数的波长参数。它的值以像素为单位制定，通常大于等于2，但不能大于输入图像尺寸的1/5.
方向(θ)：表示Gabor滤波核中平行条带的方向。有效值为从0°到360°的实数。
相位偏移(ψ)：表示Gabor核函数中余弦函数的相位参数。它的取值范围为-180°到180°。其中，0°与180°对应的方程与原点对称，-90°和90°的方程关于原点成中心对称。
长宽比(γ)：空间纵横比，决定了Gabor函数形状的椭圆率。当γ=1时，形状是圆形；当γ<1时，形状随着平行条纹方向而拉长。通常该值为0.5.
带宽(b)：Gabor滤波器的半响应空间频率带宽b和σ/λ的比率有关，其中σ表示Gabor函数的高斯因子的标准差。三者有如下关系：

σ的值不能直接设置，它仅随带宽b变换。带宽的值必须是正实数，通常为1，此时，标准差和波长的关系为 σ=0.56λ。带宽越小，标准差越大，Gabor形状越大，可见平行条纹数量越多。

python实现Gabor滤波器

# Gabor 滤波器实现
# K_size：Gabor核大小 K_size x K_size
# Sigma : σ
# Gamma： γ
# Lambda：λ
# Psi ： ψ
# angle： θ
def Gabor_filter(K_size=111, Sigma=10, Gamma=1.2, Lambda=10, Psi=0, angle=0):
	# get half size
	d = K_size // 2

	# prepare kernel
	gabor = np.zeros((K_size, K_size), dtype=np.float32)

	# each value
	for y in range(K_size):
		for x in range(K_size):
			# distance from center
			px = x - d
			py = y - d

			# degree -> radian
			theta = angle / 180. * np.pi

			# get kernel x
			_x = np.cos(theta) * px + np.sin(theta) * py

			# get kernel y
			_y = -np.sin(theta) * px + np.cos(theta) * py

			# fill kernel
			gabor[y, x] = np.exp(-(_x**2 + Gamma**2 * _y**2) / (2 * Sigma**2)) * np.cos(2*np.pi*_x/Lambda + Psi)

	# kernel normalization
	gabor /= np.sum(np.abs(gabor))

	return gabor

python做出不同角度Gabor滤波器的图像

import cv2
import numpy as np
import matplotlib.pyplot as plt


# Gabor 滤波器实现
# K_size：Gabor核大小 K_size x K_size
# Sigma : σ
# Gamma： γ
# Lambda：λ
# Psi ： ψ
# angle： θ
def Gabor_filter(K_size=111, Sigma=10, Gamma=1.2, Lambda=10, Psi=0, angle=0):
	# get half size
	d = K_size // 2

	# prepare kernel
	gabor = np.zeros((K_size, K_size), dtype=np.float32)

	# each value
	for y in range(K_size):
		for x in range(K_size):
			# distance from center
			px = x - d
			py = y - d

			# degree -> radian
			theta = angle / 180. * np.pi

			# get kernel x
			_x = np.cos(theta) * px + np.sin(theta) * py

			# get kernel y
			_y = -np.sin(theta) * px + np.cos(theta) * py

			# fill kernel
			gabor[y, x] = np.exp(-(_x**2 + Gamma**2 * _y**2) / (2 * Sigma**2)) * np.cos(2*np.pi*_x/Lambda + Psi)

	# kernel normalization
	gabor /= np.sum(np.abs(gabor))

	return gabor


# define each angle
As = [0, 45, 90, 135]

# prepare pyplot
plt.subplots_adjust(left=0, right=1, top=1, bottom=0, hspace=0, wspace=0.2)

# each angle
for i, A in enumerate(As):
 # get gabor kernel
 gabor = Gabor_filter(K_size=111, Sigma=10, Gamma=1.2, Lambda=10, Psi=0, angle=A)

 # normalize to [0, 255]
 out = gabor - np.min(gabor)
 out /= np.max(out)
 out *= 255
 
 out = out.astype(np.uint8)
 plt.subplot(1, 4, i+1)
 plt.imshow(out, cmap='gray')
 plt.axis('off')
 plt.title("Angle "+str(A))

plt.savefig("out.png")
plt.show()

实验输出Gabor滤波器图像

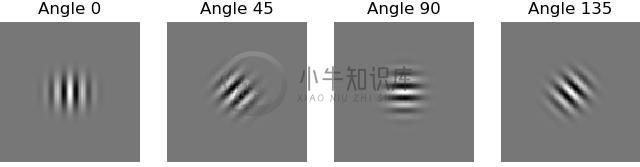
opencv（python）中使用Gabor滤波器

函数原型：

retval=cv.getGaborKernel(ksize, sigma, theta, lambd, gamma[, psi[, ktype]])

函数使用举例

import numpy as np 
import cv2 as cv 

# retval = cv.getGaborKernel(ksize, sigma, theta, lambd, gamma[, psi[, ktype]])
# Ksize 是一个元组
retval = cv.getGaborKernel(ksize=(111,111), sigma=10, theta=60, lambd=10, gamma=1.2)
image1 = cv.imread('../paojie.jpg')
# dst	=	cv.filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]])
result = cv.filter2D(image1,-1,retval)

cv.imshow('result',result)
cv.waitKey(0)
cv.destroyAllWindows()

实验结果：

参考：
python实现Gabor滤波器
Gabor滤波器参数详解
Gabor滤波器原理及opencv中的实现

到此这篇关于python Gabor滤波器讲解的文章就介绍到这了,更多相关Gabor滤波器内容请搜索小牛知识库以前的文章或继续浏览下面的相关文章希望大家以后多多支持小牛知识库！