python 经典数字滤波实例

数字滤波分为 IIR 滤波，和FIR 滤波。

FIR 滤波：

import scipy.signal as signal
import numpy as np
import pylab as pl
import matplotlib.pyplot as plt
import matplotlib
from scipy import signal
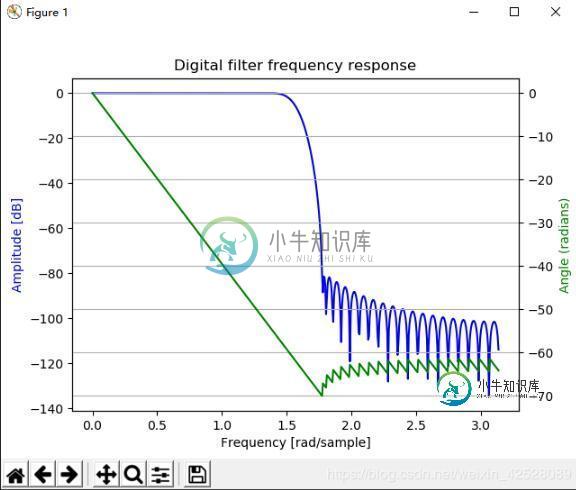
b = signal.firwin(80, 0.5, window=('kaiser', 8))
w, h = signal.freqz(b)
 
import matplotlib.pyplot as plt
fig, ax1 = plt.subplots()
ax1.set_title('Digital filter frequency response')
 
ax1.plot(w, 20 * np.log10(abs(h)), 'b')
ax1.set_ylabel('Amplitude [dB]', color='b')
ax1.set_xlabel('Frequency [rad/sample]')
 
ax2 = ax1.twinx()
angles = np.unwrap(np.angle(h))
ax2.plot(w, angles, 'g')
ax2.set_ylabel('Angle (radians)', color='g')
ax2.grid()
ax2.axis('tight')
plt.show()

运行结果：

IIR 滤波器：

from scipy import signal
import matplotlib.pyplot as plt
import matplotlib.ticker
import numpy as np
# 蓝色的是频谱图，绿色的是相位图
wp = 0.2
ws = 0.3
gpass = 1
gstop = 40
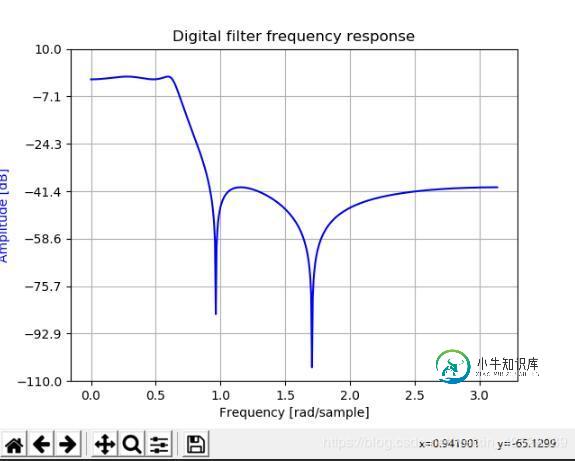
system = signal.iirdesign(wp, ws, gpass, gstop)
w, h = signal.freqz(*system)
fig, ax1 = plt.subplots()
ax1.set_title('Digital filter frequency response')
ax1.plot(w, 20 * np.log10(abs(h)), 'b')
ax1.set_ylabel('Amplitude [dB]', color='b')
ax1.set_xlabel('Frequency [rad/sample]')
ax1.grid()
ax1.set_ylim([-110, 10])
 
nticks = 8
ax1.yaxis.set_major_locator(matplotlib.ticker.LinearLocator(nticks))
 
plt.show()

运行结果：

IIR 滤波器中cheyb2 滤波器的运用

from  scipy import signal
import matplotlib.pyplot as plt
import numpy as np
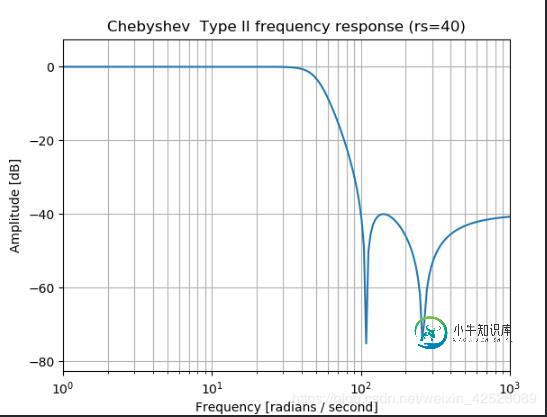
b, a = signal.cheby2(4, 40, 100, 'low', analog=True)
w, h = signal.freqs(b, a)
plt.semilogx(w, 20 * np.log10(abs(h)))#用于绘制折线图，两个函数的 x 轴、y 轴分别是指数型的。
#plt.plot(w, 20 * np.log10(abs(h)))
plt.title('Chebyshev Type II frequency response (rs=40)')
plt.xlabel('Frequency [radians / second]')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)#  not sure
plt.grid(which='both', axis='both')
 
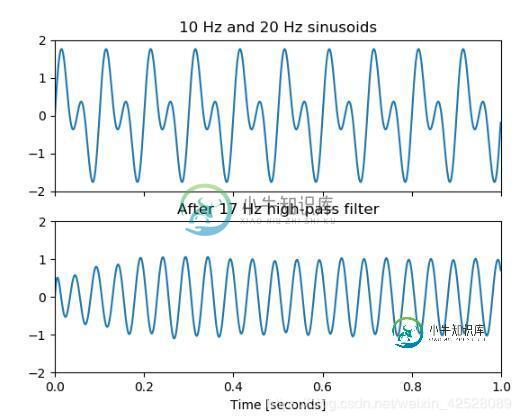
t = np.linspace(0, 1, 1000, False) # 1 second
sig = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t)
fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
ax1.plot(t, sig)
ax1.set_title('10 Hz and 20 Hz sinusoids')
ax1.axis([0, 1, -2, 2])
 
sos = signal.cheby2(12, 20, 17, 'hp', fs=1000, output='sos')
filtered = signal.sosfilt(sos, sig)
ax2.plot(t, filtered)
ax2.set_title('After 17 Hz high-pass filter')
ax2.axis([0, 1, -2, 2])
ax2.set_xlabel('Time [seconds]')
 
plt.show()

以上这篇python 经典数字滤波实例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持小牛知识库。