12.2 手写数字的识别
在上一节中,我们讨论了大量关于神经网络的理论知识,如果读者初次接触此方面的内容,可能会感到有些困惑。在进一步讨论多层感知器模型的权重学习算法(反向传播算法)之前,先将理论学习暂停片刻,看一下神经网络在实际中的应用。
 神经网络理论可以说是相当复杂的,因此作者推荐额外的两篇文献,它们更加详细地讨论了本章介绍过的一些概念:
神经网络理论可以说是相当复杂的,因此作者推荐额外的两篇文献,它们更加详细地讨论了本章介绍过的一些概念:
·T.Hastie,J.Friedman,and R.Tibshirani.The Elements of Statistical Learning,Volume 2.Springer,2009.
·C.M.Bishop et al.Pattern Recognition and Machine Learning,Volume 1.Springer New York,2006.
在本节中,通过在MNIST数据集(Mixed National Institute of Standards and Technology数据集的缩写)上对手写数字的识别,来完成我们第一个多层神经网络的训练。MNIST数据集由Yann LeCun等人创建,是机器学习算法中常用的一个基准数据集[1]。
[1] Y.LeCun,L.Bottou,Y.Bengio,and P.Haffner.Gradient-based Learning Applied to Document Recognition.Proceedings of the IEEE,86(11):2278-2324,November 1998.
12.2.1 获取MNIST数据集
MNIST数据集可通过链接http://yann.lecun.com/exdb/mnist/下载,它包含如下四个部分:
·训练集图像:train-images-idx3-ubyte.gz(9.9 MB,解压后47 MB,包含60000个样本)。
·训练集类标:train-labels-idx1-ubyte.gz(29 KB,解压后60 KB,包含60000个类标)。
·测试集图像:t10k-images-idx3-ubyte.gz(1.6 MB,解压后7.8 MB,包含10000个样本)。
·测试集类标:t10k-labels-idx1-ubyte.gz(5 KB,解压后10 KB,包含10000个类标)。
MNIST数据集基于美国国家标准与技术研究院(National Institute of Standards and Technology,NIST)的两个数据集构建而成。训练集中包含250个人的手写数字,其中50%的是高中生,另外50%来自人口调查局。测试集中的数字也是按照相同比例由高中生和人口调查局所抽选人员手写完成。
下载文件后,建议在UNIX/Linux的命令行终端窗口中,在MNIST文件所在目录,按如下命令使用gzip快速解压所下载文件:
![]()
如果读者使用的是Windows操作系统,则可以根据个人喜好选择合适的解压工具。数据集中的图像以字节形式存储,接下来,我们将其读入NumPy数组以训练和测试多层感知器模型:

load_minist函数返回两个数组,第一个为n×m维的NumPy数组(存储图像),其中n为样本数量,m为特征数量。训练数据集和测试数据集分别包含60000和10000个样本。MNIST数据集中的图像均为28×28个像素,每个像素用灰度强度值表示。在此,我们将28×28像素展开为1维行向量,并用此行向量来表示图像数组(每行或者说每个图像包含784个特征)。load_mnist函数返回的第二个数组(类标)包含对应的目标变量,即手写数字对应的类标(整数0~9)。
乍看起来,我们读取图像的方法好像有些奇怪:
![]()
为了解这两行代码是如何工作的,我们看一下MNIST网站上关于此数据集的介绍:


使用前面两行代码,在使用fromfile方法将后续字节读入NumPy数组之前,我们首先从文件缓冲区读入数据集的幻数,它是对文件协议的描述,同时读入的还有条目的数量。传递给struct.unpack函数中fmt参数的实参值:>II,此实参值包含两部分内容:
·>:这是代表大端字节序(定义多字节在计算机中的存储顺序),如果读者不熟悉大端字节序和小端字节序,可以参考维基百科中关于字节序的描述(https://en.wikipedia.org/wiki/Endianness)。
·I:代表这是一个无符号整数。
执行下列代码,我们将从解压后MNIST数据集所在目录mnist下读取60000个训练实例和10000个测试样本:

为了解MNIST数据集中图像的样子,我们通过将特征矩阵中的784像素向量还原为28×28图像,并使用matplotlib中的imshow函数将0~9数字的示例进行可视化展示:

现在我们可以看到,按照2×5方式排列的子图中显示了单个数字的图像:

此外,我们再绘制一下相同数字的多个示例,来看一下这些手写样本之间到底有多大差异:

执行上述代码后,可以看到数字7的前25个不同变体。

我们也可以选择将MNIST图像数据及其对应类标存储为CSV格式的文件,以方便不支持其原始特殊字节格式的程序使用。不过,我们应知道,CSV格式的文件会占用更多的存储空间,具体大小如下:
·train_img.csv:109.5 MB
·train_labels.csv:120 KB
·test_img.csv:18.3 MB
·test_labels:20 KB
在将MNIST数据加载到NumPy数组中后,我们可以在Python中执行如下代码,即可将数据存储为CSV格式文件:

对于已经保存过的CSV格式文件,我们可以使用NumPy的genfromtxt函数对其进行加载:

不过,加载CSV格式的MNIST数据需要更长的时间,因此建议读者尽可能使用原始的数据格式。
12.2.2 实现一个多层感知器
本小节中,我们将实现一个包含一个输入层、一个隐层和一个输出层的多层感知器,并用它来识别MNIST数据集中的图像。我们尽可能使代码做到简单易读。不过第一次接触可能会感觉稍许复杂,建议读者从Packt出版社的官网上下载本章示例代码,其中,注释和语法高亮显示使得代码更加易读。如果读者并未在IPython Notebook中运行这些代码,建议将其复制到当前工作目录下的一个Python脚本文件中,如neuralnet.py,进而可以使用如下命令在当前Python工作进程中将其导入:
![]()
代码中包含我们尚未讲解的内容,比如反向传播算法,不过其中大部分代码都是基于第2章中自适应线性神经元(Adaline)实现的,因此读起来应该比较熟悉。如果有不理解的代码也不必担心,我们将在本章后续内容中进行讲解。不过,在当前阶段先熟悉代码有利于理解后面理论部分内容。



现在,我们来初始化一个784-50-10的感知器模型,该神经网络包含784个输入单元(n_features),50个隐层单元(n_hidden),以及10个输出单元(n_output):

读者也许已经注意到,在重复实现多层感知器的同时,我们还额外实现了一些功能,总结如下:
·l2:L2正则化系数λ,用于降低过拟合程度,类似地,l1对应L1正则化参数λ。
·epochs:遍历训练集的次数(迭代次数)。
·eta:学习速率η。
·alpha:动量学习进度的参数,它在上一轮迭代的基础上增加一个因子,用于加快权重更新的学习Δwt=η▽J(wt+Δwt-1)(其中,t为当前所在的步骤,也就是当前迭代次数)。
·decrease_const:用于降低自适应学习速率n的常数d,随着迭代次数的增加而随之递减以更好地确保收敛。
·shuffle:在每次迭代前打乱训练集的顺序,以防止算法陷入死循环。
·Minibatches:在每次迭代中,将训练数据划分为k个小的批次,为加速学习的过程,梯度由每个批次分别计算,而不是在整个训练数据集上进行计算。
接下来,我们将使用重排后的MNIST训练数据集中的60000个样本来训练多层感知器。执行下列代码前请注意:在当前主流配置的台式计算机上,训练神经网络所需的时间大约为10~30分钟:
![]()
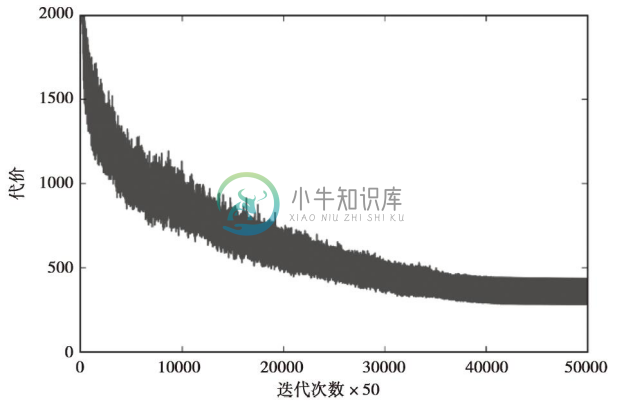
与前面自适应线性神经元的实现类似,我们使用cost_列表保存了每轮迭代中的代价并且可以进行可视化,以确保优化算法能够收敛。在此,我们仅绘制了50个子批次的每50次迭代的结果(50个子批次×1000次迭代)。代码如下:

通过下图可见,代价函数的图像中有很明显的噪声。这是由于我们使用了随机梯度下降算法的一个变种(子批次学习),来训练神经网络所造成的。
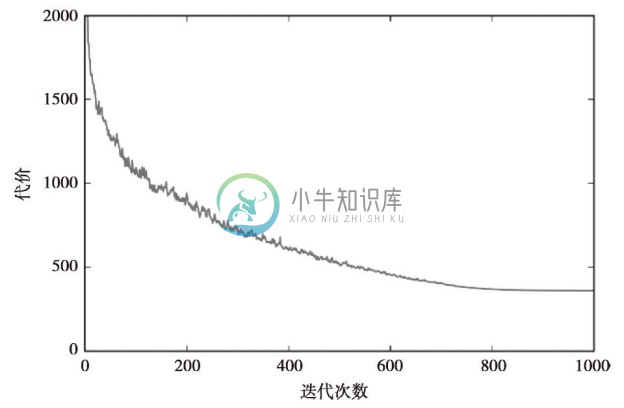
虽然通过上图可以看出,优化算法在经过大约800(40000/50=800)轮迭代后收敛,使用所有子批次的平均值,我们绘制出了一个相对平滑的代价函数图像。代码如下:

从下图可以清楚地看出,训练算法在经过约800次迭代后随即收敛:
现在,我们通过计算预测精度来评估模型的性能:

正如我们所见,模型能够正确识别大部分的训练数字,不过现在还不知道将其泛化到未知数据上的效果如何?我们来计算一下模型在测试数据集上10000个图像上的准确率:

由于模型在训练集与测试集上的精度仅有微小的差异,我们可以推断,模型对于训练数据仅轻微地过拟合。为了进一步对模型进行调优,我们可以改变隐层单元的数量、正则化参数的值、学习速率、衰减常数的值,或者使用第6章中介绍过的自适应学习等技术(此问题留给读者作为练习作业)。
现在,我们看一下多层感知器难以处理的一些图像:


我们得到一个包含5×5子图矩阵的图像,每个子图标题中的第一个数字为图像索引,第二个数字为真实的类标(t),第三个数字则是预测的类标(p)。

从上图可以看出,某些图像即便让我们人工去分类也存在一定难度。例如,数字9的下部呈弯钩状,因此被识别成3或者8(参见第3、16和17子图)。

