5.2 通过线性判别分析压缩无监督数据

优质

小牛编辑

123浏览

2023-12-01

线性判别分析（Linear Discriminant Analysis，LDA）是一种可作为特征抽取的技术，它可以提高数据分析过程中的计算效率，同时，对于不适用于正则化的模型，它可以降低因维度灾难带来的过拟合。

LDA的基本概念与PCA非常相似，PCA试图在数据集中找到方差最大的正交的主成分分量的轴，而LDA的目标是发现可以最优化分类的特征子空间。LDA与PCA都是可用于降低数据集维度的线性转换技巧。其中，PCA是无监督算法，而LDA是监督算法。因此，我们可以这样直观地认为：与PCA相比，LDA是一种更优越的用于分类的特征提取技术。但是A.M.Martinez提出：在图像识别任务中的某些情况下，如每个类别中只有少量样本，使用PCA作为预处理工具的分类结果更佳^[1]。

LDA有时也被称作Fisher抯LDA，Ronald A.Fisher于1936年针对二类别分类问题对Fisher线性判别（Fisher抯Linear Discriminant）做了最初的形式化^[2]。1948年，基于类别方差相等和类内样本呈标准正态分布的假设，Radhakrishna Rao将Fisher抯LDA泛化到了多类别分类问题上，即我们现在所说的LDA^[3]。

下图解释了二类别分类中LDA的概念。类别1、类别2中的样本分别用叉号和原点来表示：

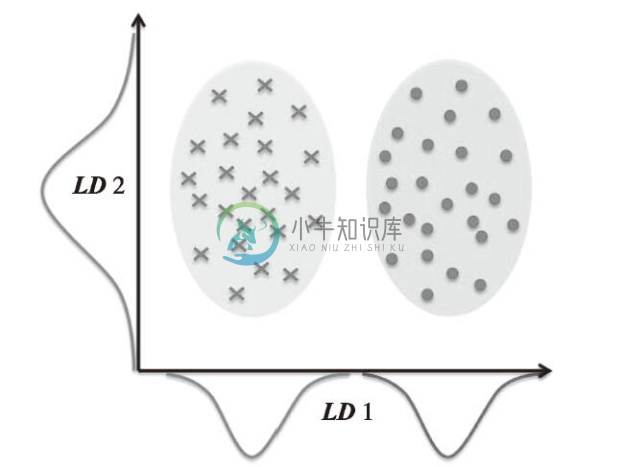
如上图所示，在x轴方向（LD1），通过线性判定，可以很好地将呈正态分布的两个类分开。虽然沿y轴（LD2）方向的线性判定保持了数据集的较大方差，但是沿此方向无法提供关于类别区分的任何信息，因此它不是一个好的线性判定。

一个关于LDA的假设就是数据呈正态分布。此外，我们还假定各类别中数据具有相同的协方差矩阵，且样本的特征从统计上来讲是相互独立的。不过，即使一个或多个假设没有满足，LDA仍旧可以很好地完成降维工作^[4]。

在进入下一节详细讨论LDA的原理之前，我们先来总结一下LDA方法的关键步骤：

1）对d维数据集进行标准化处理（d为特征的数量）。

2）对于每一类别，计算d维的均值向量。

3）构造类间的散布矩阵S_B以及类内的散布矩阵S_W。

4）计算矩阵的特征值及对应的特征向量。

5）选取前k个特征值所对应的特征向量，构造一个d×k维的转换矩阵W，其中特征向量以列的形式排列。

6）使用转换矩阵W将样本映射到新的特征子空间上。

特征呈正态分布且特征间相互独立是我们使用LDA时所做的假设。同时，LDA算法假定各个类别的协方差矩阵是一致的。然而，即使我们违背了上述假设，LDA算法仍旧能很好地完成数据降维及分类任务（R.O.Duda,P.E.Hart，and D.G.Stork.Pattern Classification.2nd.Edition.New York,2001）。

[1] A.M.Martinez and A.C.Kak.PCA Versus LDA.Pattern Analysis and Machine Intelligence，IEEE Transactions on，23（2）：228-233,2001.

[2] R.A. Fisher.The Use of Multiple Measuremengts in Taxonomic Problems.Annals of Eugenics，7(2):179-188，1936.

[3] C. R. Rao. The Utilization of Multiple Measurements in Problems of Biological Classification. Journal of the Royal Statistical Society. Series B（Methodological），10(2):159—203，1948.

[4] R. O. Duda, P. E. Hart, and D. G. Stork. Pattern Classification. 2nd. Edition. New York, 2001.

5.2.1　计算散布矩阵

本节伊始，在讲解PCA时就对葡萄酒数据集做了标准化处理，因此我们将跳过第一步直接计算均值向量，计算中，我们将分别构建类内散布矩阵和类间散布矩阵。均值向量m_i存储了类别i中样本的特征均值μ_m：

葡萄酒数据集的三个类别对应三个均值向量：

通过均值向量，我们来计算一下类内散布矩阵S_W：

这可以通过累加各类别i的散布矩阵S_i来计算：

此前我们对散布矩阵进行计算时，曾假设训练集的类标是均匀分布的。但是，通过打印类标的数量，可以看到在此并未遵循此假设：

因此，在我们通过累加方式计算散布矩阵S_W前，需要对各类别的散布矩阵S_i做缩放处理。当我们用各类别单独的散布矩阵除以此类别内样本数量N_i时，可以发现计算散布矩阵的方式与计算协方差矩阵的方式是一致的。协方差矩阵可以看作是归一化的散布矩阵：

在完成类内散布矩阵（或协方差矩阵）的计算后，我们进入下一步骤，计算类间散布矩阵S_B：

其中，m为全局均值，它在计算时用到了所有类别中的全部样本：

5.2.2　在新特征子空间上选取线性判别算法

LDA余下的步骤与PCA的步骤相似。不过，这里我们不对协方差矩阵做特征分解，而是求解矩阵的广义特征值：

在求得了特征对之后，我们按照降序对特征值进行排序：

熟悉线性代数的读者应该知道：d×d维协方差矩阵的秩最大为d-1，而且确实可以发现，我们只得到了两个非零特征值（实际得到的第3～13个特征值并非完全为零，而是趋近于0的实数，这个结果是由NumPy浮点运算导致的）。请注意，在极少的情况下可达到完美的共线性（所有样本的点落在一条直线上），这时协方差矩阵的秩为1，将导致矩阵只有一个含非零特征值的特征向量。

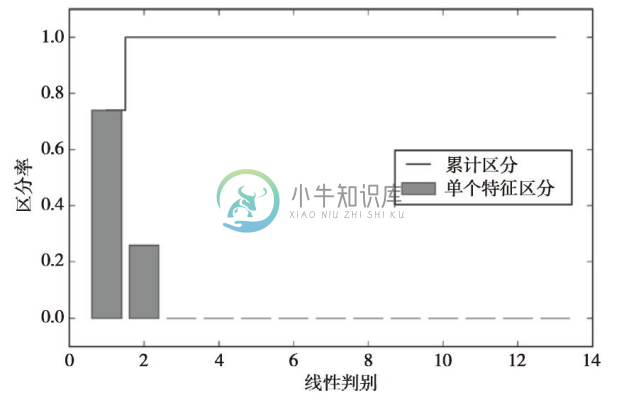
为了度量线性判别（特征向量）可以获取多少可区分类别的信息，与前面PCA小节中对累计方差的绘制类似，我们按照特征值降序绘制出特征对线性判别信息保持程度的图像。为了简便起见，我们在此使用了判定类别区分能力的相关信息discriminability。