线性判别分析逆变换

Question

我尝试使用scikit-learn库中的线性判别分析，以便对具有200多个功能的数据进行降维处理。但是我inverse_transform在LDA类中找不到该函数。

我只是想问，如何从LDA域中的某个点重建原始数据？

编辑基于@bogatron和@kazemakase的答案：

我认为“原始数据”一词是错误的，我应该使用“原始坐标”或“原始空间”。我知道没有所有PCA都无法重建 原始数据
，但是当我们构建形状空间时，我们将借助PCA将数据投影到较低维度。PCA尝试仅使用2个或3个分量来解释数据，这些分量可以捕获数据的大部分差异，如果我们根据它们重构数据库，它应该向我们显示导致这种分离的形状部分。

我再次检查了scikit-learn
LDA的源代码，并且发现特征向量存储在scalings_变量中。当使用svd求解器时，不可能对特征向量（scalings_）矩阵进行逆运算，但是当我尝试对矩阵进行伪逆运算时，可以重构形状。

这里，有两个分别从[4.28，0.52]和[0，0]点重构的图像：

我认为，如果有人深入解释LDA逆变换的数学局限性，那就太好了。

Answer 1

LDA的倒数不一定有意义，因为它会丢失很多信息。

为了进行比较，请考虑PCA。在这里，我们得到一个系数矩阵，用于转换数据。我们可以通过从矩阵中剥离行来进行降维。为了获得逆变换，我们 首先对整个
矩阵求逆，然后删除与删除的行相对应的列。

LDA没有提供完整的矩阵。我们只能得到一个不能直接求逆的简化矩阵。可以采用伪逆，但是这比我们拥有完整矩阵时要低得多。

考虑一个简单的例子：

C = np.ones((3, 3)) + np.eye(3)  # full transform matrix
U = C[:2, :]  # dimensionality reduction matrix
V1 = np.linalg.inv(C)[:, :2]  # PCA-style reconstruction matrix
print(V1)
#array([[ 0.75, -0.25],
#       [-0.25,  0.75],
#       [-0.25, -0.25]])

V2 = np.linalg.pinv(U)  # LDA-style reconstruction matrix
print(V2)
#array([[ 0.63636364, -0.36363636],
#       [-0.36363636,  0.63636364],
#       [ 0.09090909,  0.09090909]])

如果我们有完整的矩阵，则得到的逆变换（V1）与简单地变换（）的逆变换不同V2。 这是因为在第二种情况下，我们丢失了有关废弃组件的所有信息。

你被警告了。如果您仍然想进行逆LDA转换，请使用以下函数：

import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from sklearn.utils.validation import check_is_fitted
from sklearn.utils import check_array, check_X_y

import numpy as np


def inverse_transform(lda, x):
    if lda.solver == 'lsqr':
        raise NotImplementedError("(inverse) transform not implemented for 'lsqr' "
                                  "solver (use 'svd' or 'eigen').")
    check_is_fitted(lda, ['xbar_', 'scalings_'], all_or_any=any)

    inv = np.linalg.pinv(lda.scalings_)

    x = check_array(x)
    if lda.solver == 'svd':
        x_back = np.dot(x, inv) + lda.xbar_
    elif lda.solver == 'eigen':
        x_back = np.dot(x, inv)

    return x_back


iris = datasets.load_iris()

X = iris.data
y = iris.target
target_names = iris.target_names

lda = LinearDiscriminantAnalysis()
Z = lda.fit(X, y).transform(X)

Xr = inverse_transform(lda, Z)

# plot first two dimensions of original and reconstructed data
plt.plot(X[:, 0], X[:, 1], '.', label='original')
plt.plot(Xr[:, 0], Xr[:, 1], '.', label='reconstructed')
plt.legend()

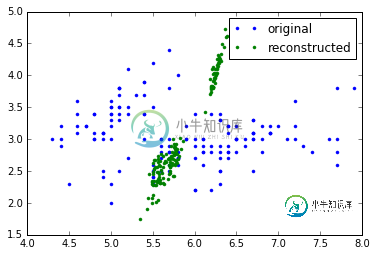
您会看到，逆变换的结果与原始数据没有多大关系（嗯，有可能猜测投影的方向）。变体的相当一部分永久消失了。