八、无监督学习第二部分：聚类

优质

小牛编辑

133浏览

2023-12-01

聚类是根据一些预定义的相似性或距离（相异性）度量（例如欧氏距离），将样本收集到相似样本分组中的任务。

在本节中，我们将在一些人造和真实数据集上，探讨一些基本聚类任务。

以下是聚类算法的一些常见应用：

用于数据减少的压缩
将数据汇总为推荐系统的再处理步骤
相似性：
- 分组相关的网络新闻（例如 Google 新闻）和网络搜索结果
- 为投资组合管理分组相关股票报价
- 为市场分析建立客户档案
为无监督特征提取构建原型样本的代码簿

让我们从创建一个简单的二维人造数据集开始：

from sklearn.datasets import make_blobs

X, y = make_blobs(random_state=42)
X.shape

plt.figure(figsize=(8, 8))
plt.scatter(X[:, 0], X[:, 1])

在上面的散点图中，我们可以看到三组不同的数据点，我们希望使用聚类来恢复它们 - 想一想“检测”类标签，我们在分类任务中认为它们是理所当然的。

即使这些分组在数据中是显而易见的，当数据存在于高维空间中时很难发现它们，我们无法在单个直方图或散点图中可视化。

现在我们将使用最简单的聚类算法之一，K-means。这是一种迭代算法，其搜索三个簇中心，使得从每个点到其簇中心的距离最小。 K-means 的标准实现使用欧几里德距离，这就是为什么，如果我们使用真实世界的数据集，我们要确保所有变量都以相同的比例进行测量。在之前的笔记本中，我们讨论了实现这一目标的一种技术，即标准化。

问题
你期望输出看起来像什么？

from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=3, random_state=42)

我们可以通过调用fit然后访问KMeans估计器的labels_属性，或者通过调用fit_predict来获取簇标签。无论哪种方式，结果都包含分配给每个点的簇的 ID。

labels = kmeans.fit_predict(X)

labels

np.all(y == labels)

让我们可视化已发现的分配：

plt.figure(figsize=(8, 8))
plt.scatter(X[:, 0], X[:, 1], c=labels)

与真实标签相比：

plt.figure(figsize=(8, 8))
plt.scatter(X[:, 0], X[:, 1], c=y)

在这里，我们可能对聚类结果感到满意。但总的来说，我们可能希望具有更加量化的评估。如何将我们的簇标签与生成 blob 时得到的真实情况进行比较？

from sklearn.metrics import confusion_matrix, accuracy_score

print('Accuracy score:', accuracy_score(y, labels))
print(confusion_matrix(y, labels))

np.mean(y == labels)

练习在查看“真实”标签数组y，以及上面的散点图和labels之后，你能理解为什么我们的计算精度为 0.0 而不是 1.0 吗，你能解决它吗？

即使我们完全恢复了数据的簇划分，我们分配的簇 ID 也是任意的，我们不能希望恢复它们。因此，我们必须使用不同的评分指标，例如adjusted_rand_score，它对标签的排列不变：

from sklearn.metrics import adjusted_rand_score

adjusted_rand_score(y, labels)

K-means 的“缺点”之一是我们必须指定簇的数量，这是我们通常事先不知道的。例如，让我们看一下如果我们在人造 3-blob 数据集中，将簇数设置为 2 会发生什么：

kmeans = KMeans(n_clusters=2, random_state=42)
labels = kmeans.fit_predict(X)
plt.figure(figsize=(8, 8))
plt.scatter(X[:, 0], X[:, 1], c=labels)

kmeans.cluster_centers_

Elbow 方法

Elbow方法是一种“经验法则”，用于查找最佳簇数。在这里，我们看一下不同 k 值的聚类散度：

distortions = []
for i in range(1, 11):
    km = KMeans(n_clusters=i, 
                random_state=0)
    km.fit(X)
    distortions.append(km.inertia_)

plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.show()

然后，我们选择类似“elbow 的凹陷”的值。我们可以看到，在这种情况下，这是k = 3，给定我们先前对数据集的视觉预期，这是有意义的。

聚类具有以下假设：聚类算法通过假设样本应该分组到一起，来找到簇。每种算法都会做出不同的假设，结果的质量和可解释性将取决于你的目标是否满足假设。对于 K 均值聚类，模型是所有簇具有相等的球形方差。

通常，无法保证聚类算法找到的结构，与你感兴趣的内容有任何关系。

我们可以轻松地创建一个数据集，具有非各向同性的簇的，其中 kmeans 将失败：

plt.figure(figsize=(12, 12))

n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)

# 簇的数量不正确
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X)

plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("Incorrect Number of Blobs")

# 各向异性分布的数据
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)

plt.subplot(222)
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
plt.title("Anisotropicly Distributed Blobs")

# 不同的方差
X_varied, y_varied = make_blobs(n_samples=n_samples,
                                cluster_std=[1.0, 2.5, 0.5],
                                random_state=random_state)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)

plt.subplot(223)
plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("Unequal Variance")

# 大小不均匀的 blobs
X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:10]))
y_pred = KMeans(n_clusters=3,
                random_state=random_state).fit_predict(X_filtered)

plt.subplot(224)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs")

一些值得注意的聚类例程

以下是两种众所周知的聚类算法。

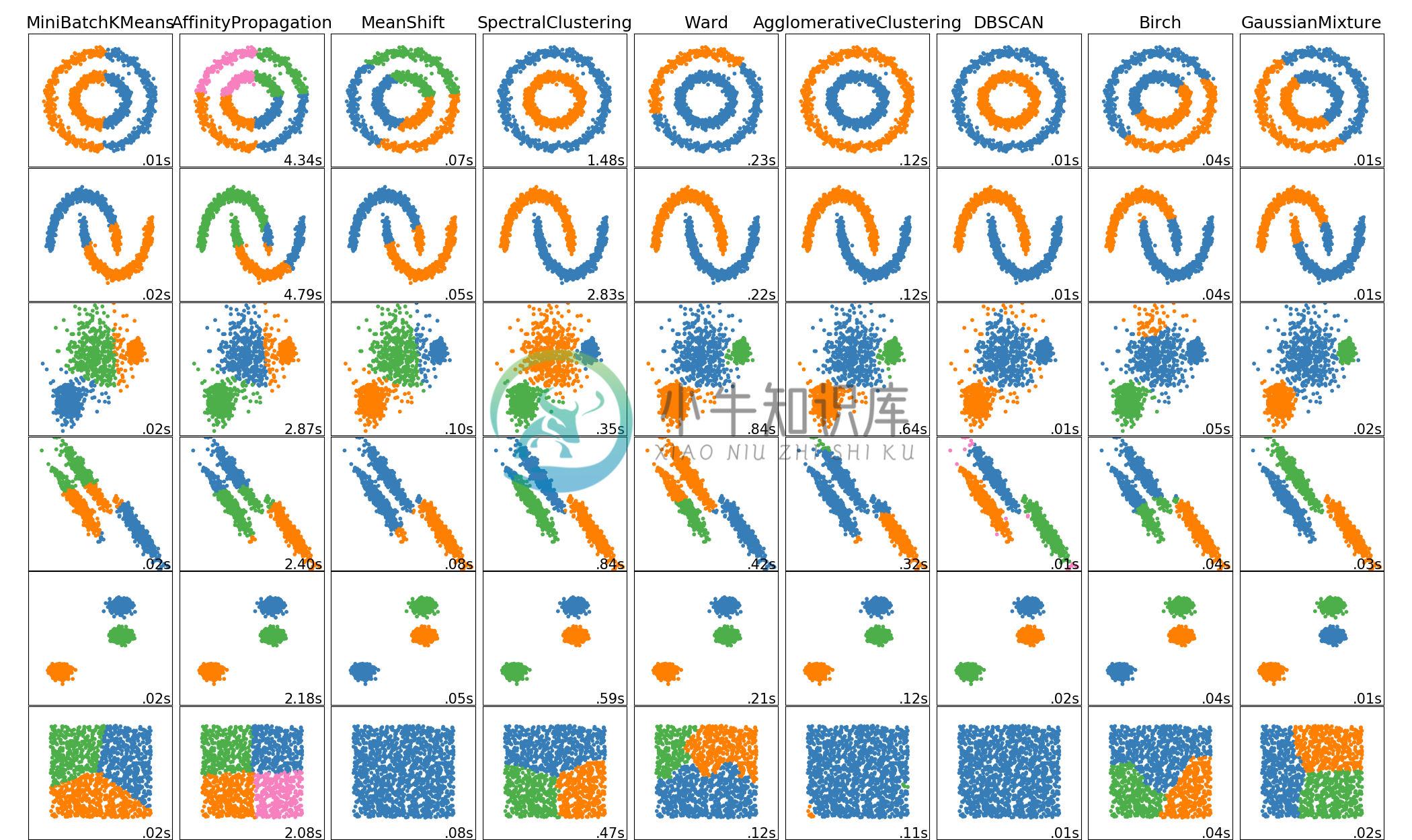
sklearn.cluster.KMeans：最简单但有效的聚类算法。需要事先提供簇数，并假设数据为输入而标准化（但使用 PCA 模型作为预处理器）。
sklearn.cluster.MeanShift：可以找到比 KMeans 更好看的簇，但不能扩展到大量样本。
sklearn.cluster.DBSCAN：可以基于密度检测不规则形状的簇，即输入空间中的稀疏区域可能变成簇间边界。还可以检测异常值（不属于簇的样本）。
sklearn.cluster.AffinityPropagation：基于数据点间消息传递的聚类算法。
sklearn.cluster.SpectralClustering：应用于归一化图拉普拉斯算子的投影的 KMeans：如果亲和度矩阵被解释为图的邻接矩阵，则找到归一化的图切割。
sklearn.cluster.Ward： Ward基于Ward算法实现层次聚类，Ward算法是一种方差最小化方法。在每个步骤中，它最小化所有簇内的平方差异的总和（惯性标准）。

其中，Ward，SpectralClustering，DBSCAN和AffinityPropagation也可以与预先计算的相似性矩阵一起使用。

练习：数字聚类
对数字数据执行 K-means 聚类，搜索十个簇。将簇中心可视化为图像（即，将每个聚类中心形状变为 8x8 并使用plt.imshow。）簇是否与特定数字相关？什么是adjusted_rand_score？可视化上个笔记本中的投影数字，但这次使用簇标签作为颜色。你注意到了什么？

from sklearn.datasets import load_digits
digits = load_digits()
# ...

# %load solutions/08B_digits_clustering.py