二十、无监督学习:层次和基于密度的聚类算法
在第八章中,我们介绍了一种必不可少且广泛使用的聚类算法 K-means。 K-means 的一个优点是它非常容易实现,并且与其他聚类算法相比,它在计算上也非常有效。 然而,我们已经看到 K-Means 的一个缺点是它只有在数据可以分组为球形时才能正常工作。 此外,我们必须事先指定簇的数量k - 如果我们没有我们期望找到多少个簇的先验知识,这可能是一个问题。
在本笔记本中,我们将介绍两种可选的聚类方法,层次聚类和基于密度的聚类。
层次聚类
层次聚类的一个很好的特性是,我们可以将结果可视化为树状图,即层次树。 使用可视化,我们可以通过设置“深度”阈值来决定我们希望数据集的簇有多“深”。 或者换句话说,我们不需要预先决定簇的数量。
聚合和分裂的层次聚类
此外,我们可以区分两种主要的层次聚类方法:分裂聚类和聚合聚类。 在聚合聚类中,我们从数据集中的单个样本开始,并迭代地将其与其他样本合并以形成簇 - 我们可以将其视为构建簇的树状图的自底向上的方法。 然而,在分裂聚类中,我们从作为一个簇的整个数据集开始,并且我们迭代地将其拆分成更小的子簇 - 自顶向下的方法。
在这个笔记本中,我们将使用聚合聚类。
单个和完整链接
现在,下一个问题是我们如何测量样本之间的相似性。 一种方法是我们已经在 K-Means 算法中使用的,熟悉的欧几里德距离度量。 作为回顾,两个m维向量p和q之间的距离可以计算为:
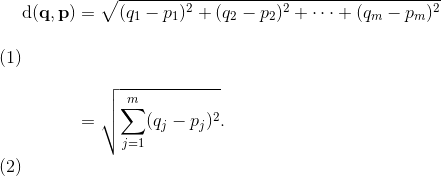
然而,这是两个个样本之间的距离。 现在,我们如何计算样本子集之间的相似性,以便在构建树状图时决定合并哪些簇? 即,我们的目标是迭代地合并最相似的一对簇,直到只剩下一个大簇。 有许多不同的方法,例如单个和完整链接。
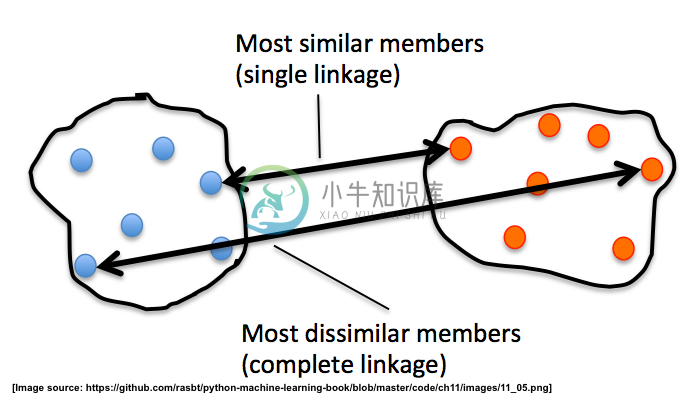
在单个链接中,我们在每两个簇中选取一对最相似的样本(例如,基于欧几里德距离),并将具有最相似的两个成员的两个簇合并为一个新的更大的簇。
在完整链接中,我们比较每两个簇的两个最不相似的成员,并且我们合并两个簇,其中两个最不相似的成员之间的距离最小。
译者注:还有比较两个簇形心的方法,算是一种折中。
为了看到实际的聚合层次聚类方法,让我们加载熟悉的鸢尾花数据集 - 我们假装不知道真正的类标签,并想要找出它包含多少不同的物种:
from sklearn.datasets import load_iris
from figures import cm3
iris = load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
n_samples, n_features = X.shape
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cm3)
首先,我们从一些探索性聚类开始,使用 SciPy 的linkage和dendrogram函数来可视化簇的树状图:
from scipy.cluster.hierarchy import linkage
from scipy.cluster.hierarchy import dendrogram
clusters = linkage(X,
metric='euclidean',
method='complete')
dendr = dendrogram(clusters)
plt.ylabel('Euclidean Distance')
接下来,让我们使用来自 scikit-learn 的AgglomerativeClustering估计器,并将数据集划分为 3 个簇。你能猜出它会重现的树状图中有哪 3 个簇吗?
from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=3,
affinity='euclidean',
linkage='complete')
prediction = ac.fit_predict(X)
print('Cluster labels: %s\n' % prediction)
plt.scatter(X[:, 0], X[:, 1], c=prediction, cmap=cm3)
基于密度的聚类 - DBSCAN
另一种有用的聚类方法是“具有噪声的基于密度的聚类方法”(DBSCAN)。 本质上,我们可以将 DBSCAN 视为一种算法,该算法根据密集的点区域将数据集划分为子分组。
在 DBSCAN 中,我们区分了 3 种不同的“点”:
- 核心点:核心点是一个点,在其半径
epsilon内,至少具有最小数量(MinPts)的其他点。 - 边界点:边界点是一个点,它不是核心点,因为它的邻域中没有足够的
MinPts,但位于核心点的半径epsilon内。 - 噪点:所有其他的点,既不是核心点也不是边界点。
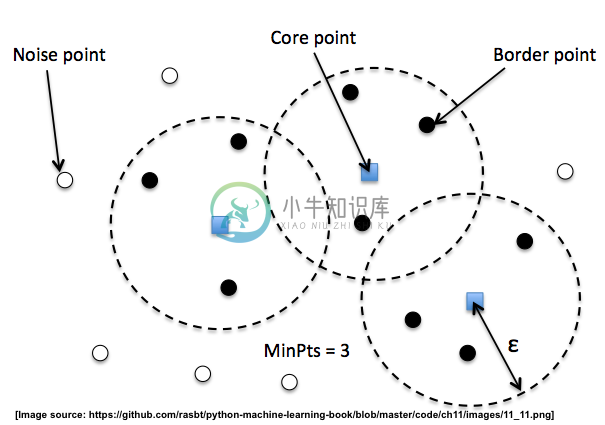
DBSCAN 的一个很好的特性是我们不必预先指定多少个簇。 但是,它需要设置其他超参数,例如MinPts的值和半径epsilon。
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=400,
noise=0.1,
random_state=1)
plt.scatter(X[:,0], X[:,1])
plt.show()
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=0.2,
min_samples=10,
metric='euclidean')
prediction = db.fit_predict(X)
print("Predicted labels:\n", prediction)
plt.scatter(X[:, 0], X[:, 1], c=prediction, cmap=cm3)
练习
使用以下玩具数据集,两个同心圆,尝试我们到目前为止使用的三种不同的聚类算法:
KMeans,AgglomerativeClustering和DBSCAN。 哪种聚类算法能够最好地再现或发现隐藏的结构(假装我们不知道y)? 你能解释为什么这个特殊的算法是一个不错的选择,而另外两个“失败”了?
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1500,
factor=.4,
noise=.05)
plt.scatter(X[:, 0], X[:, 1], c=y);
# %load solutions/20_clustering_comparison.py

