Python聚类算法之凝聚层次聚类实例分析
本文实例讲述了Python聚类算法之凝聚层次聚类。分享给大家供大家参考,具体如下:
凝聚层次聚类:所谓凝聚的,指的是该算法初始时,将每个点作为一个簇,每一步合并两个最接近的簇。另外即使到最后,对于噪音点或是离群点也往往还是各占一簇的,除非过度合并。对于这里的“最接近”,有下面三种定义。我在实现是使用了MIN,该方法在合并时,只要依次取当前最近的点对,如果这个点对当前不在一个簇中,将所在的两个簇合并就行:
单链(MIN):定义簇的邻近度为不同两个簇的两个最近的点之间的距离。
全链(MAX):定义簇的邻近度为不同两个簇的两个最远的点之间的距离。
组平均:定义簇的邻近度为取自两个不同簇的所有点对邻近度的平均值。
# scoding=utf-8
# Agglomerative Hierarchical Clustering(AHC)
import pylab as pl
from operator import itemgetter
from collections import OrderedDict,Counter
points = [[int(eachpoint.split('#')[0]), int(eachpoint.split('#')[1])] for eachpoint in open("points","r")]
# 初始时每个点指派为单独一簇
groups = [idx for idx in range(len(points))]
# 计算每个点对之间的距离
disP2P = {}
for idx1,point1 in enumerate(points):
for idx2,point2 in enumerate(points):
if (idx1 < idx2):
distance = pow(abs(point1[0]-point2[0]),2) + pow(abs(point1[1]-point2[1]),2)
disP2P[str(idx1)+"#"+str(idx2)] = distance
# 按距离降序将各个点对排序
disP2P = OrderedDict(sorted(disP2P.iteritems(), key=itemgetter(1), reverse=True))
# 当前有的簇个数
groupNum = len(groups)
# 过分合并会带入噪音点的影响,当簇数减为finalGroupNum时,停止合并
finalGroupNum = int(groupNum*0.1)
while groupNum > finalGroupNum:
# 选取下一个距离最近的点对
twopoins,distance = disP2P.popitem()
pointA = int(twopoins.split('#')[0])
pointB = int(twopoins.split('#')[1])
pointAGroup = groups[pointA]
pointBGroup = groups[pointB]
# 当前距离最近两点若不在同一簇中,将点B所在的簇中的所有点合并到点A所在的簇中,此时当前簇数减1
if(pointAGroup != pointBGroup):
for idx in range(len(groups)):
if groups[idx] == pointBGroup:
groups[idx] = pointAGroup
groupNum -= 1
# 选取规模最大的3个簇,其他簇归为噪音点
wantGroupNum = 3
finalGroup = Counter(groups).most_common(wantGroupNum)
finalGroup = [onecount[0] for onecount in finalGroup]
dropPoints = [points[idx] for idx in range(len(points)) if groups[idx] not in finalGroup]
# 打印规模最大的3个簇中的点
group1 = [points[idx] for idx in xrange(len(points)) if groups[idx]==finalGroup[0]]
group2 = [points[idx] for idx in xrange(len(points)) if groups[idx]==finalGroup[1]]
group3 = [points[idx] for idx in xrange(len(points)) if groups[idx]==finalGroup[2]]
pl.plot([eachpoint[0] for eachpoint in group1], [eachpoint[1] for eachpoint in group1], 'or')
pl.plot([eachpoint[0] for eachpoint in group2], [eachpoint[1] for eachpoint in group2], 'oy')
pl.plot([eachpoint[0] for eachpoint in group3], [eachpoint[1] for eachpoint in group3], 'og')
# 打印噪音点,黑色
pl.plot([eachpoint[0] for eachpoint in dropPoints], [eachpoint[1] for eachpoint in dropPoints], 'ok')
pl.show()
运行效果截图如下:
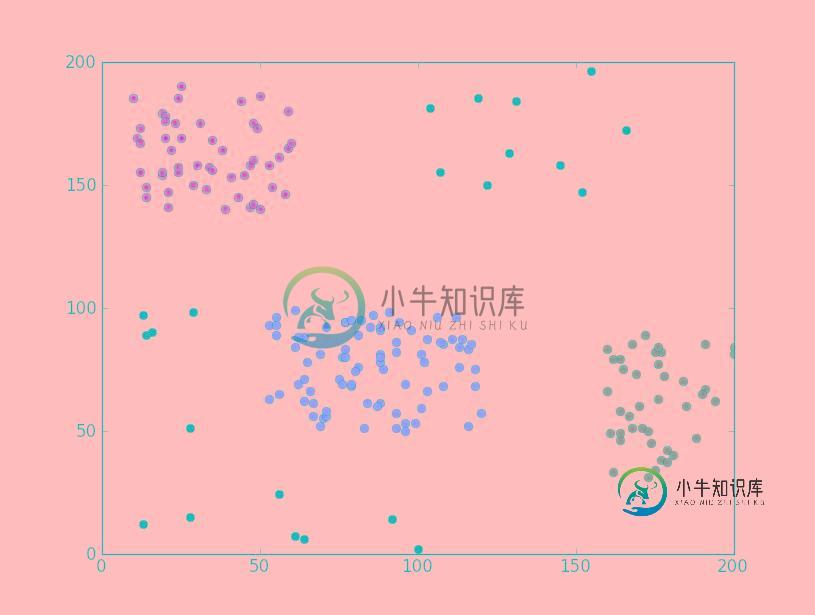
希望本文所述对大家Python程序设计有所帮助。
-
对于层次聚类法,我们不需要预先指定分类的数量,这个算方法会将每条数据都当作是一个分类,每次迭代的时候合并距离最近的两个分类,直到剩下一个分类为止。 因此聚类的结果是:顶层有一个大分类,这个分类下有两个子分类,每个子分类下又有两个子分类,依此类推,层次聚类也因此得命。 在合并的时候我们会计算两个分类之间的距离,可以采用不同的方法。如下图中的A、B、C三个分类,我们应该将哪两个分类合并起来呢? 单链聚
-
我们可以使用优先队列来实现这个聚类算法。 什么是优先队列呢? 普通的队列有“先进先出”的规则,比如向队列先后添加Moa、Suzuka、Yui,取出时得到的也是Moa、Suzuka、Yui: 而对于优先队列,每个元素都可以附加一个优先级,从队列中取出时会得到优先级最高的元素。比如说,我们定义年龄越小优先级越高,以下是插入过程: 取出的第一个元素是Yui,因为她的年龄最小: 我们看看Python中如何
-
本文向大家介绍Python聚类算法之DBSACN实例分析,包括了Python聚类算法之DBSACN实例分析的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了Python聚类算法之DBSACN。分享给大家供大家参考,具体如下: DBSCAN:是一种简单的,基于密度的聚类算法。本次实现中,DBSCAN使用了基于中心的方法。在基于中心的方法中,每个数据点的密度通过对以该点为中心以边长为2*EPs的
-
使用k-means算法时需要指定分类的数量,这也是算法名称中“k”的由来。 k-means是Lloyd博士在1957年提出的,虽然这个算法已有50年的历史,但却是当前最流行的聚类算法! 下面让我们来了解一下k-means聚类过程: 我们想将图中的记录分成三个分类(即k=3),比如上文提到的犬种数据,坐标轴分别是身高和体重。 由于k=3,我们随机选取三个点来作为聚类的起始点(分类的中心点),并用红黄
-
算法介绍 K-Means又名为K均值算法,他是一个聚类算法,这里的K就是聚簇中心的个数,代表数据中存在多少数据簇。K-Means在聚类算法中算是非常简单的一个算法了。有点类似于KNN算法,都用到了距离矢量度量,用欧式距离作为小分类的标准。 算法步骤 (1)、设定数字k,从n个初始数据中随机的设置k个点为聚类中心点。 (2)、针对n个点的每个数据点,遍历计算到k个聚类中心点的距离,最后按照离哪个中心
-
本文向大家介绍Python实现Kmeans聚类算法,包括了Python实现Kmeans聚类算法的使用技巧和注意事项,需要的朋友参考一下 本节内容:本节内容是根据上学期所上的模式识别课程的作业整理而来,第一道题目是Kmeans聚类算法,数据集是Iris(鸢尾花的数据集),分类数k是3,数据维数是4。 关于聚类 聚类算法是这样的一种算法:给定样本数据Sample,要求将样本Sample中相似的

