11.2 层次聚类

在本节，我们将学习另一种基于原型的聚类：层次聚类（hierarchical clustering）。层次聚类算法的一个优势在于：它能够使我们绘制出树状图（dendrogram，基于二叉层次聚类的可视化），这有助于我们使用有意义的分类法解释聚类结果。层次聚类的另一优势在于我们无需事先指定簇数量。

层次聚类有两种主要方法：凝聚（agglomerative）层次聚类和分裂（divisive）层次聚类。在分裂层次聚类中，我们首先把所有样本看作是在同一个簇中，然后迭代地将簇划分为更小的簇，直到每个簇只包含一个样本。本节我们将主要介绍凝聚层次聚类，它与分裂层次聚类相反，最初我们把每个样本都看作是一个单独的簇，重复地将最近的一对簇进行合并，直到所有的样本都在一个簇中为止。

在凝聚层次聚类中，判定簇间距离的两个标准方法分别是单连接（single linkage）和全连接（complete linkage）。我们可以使用单连接方法计算每一对簇中最相似两个样本的距离，并合并距离最近的两个样本所属簇。与之相反，全连接的方法是通过比较找到分布于两个簇中最不相似的样本（距离最远的样本），进而完成簇的合并。如下图所示：

凝聚层次聚类中其他常用的算法还有平均连接（average linkage）和ward连接（Ward抯linkage）。使用平均连接时，合并两个簇间所有成员间平均距离最小的两个簇。当使用ward连接时，被合并的是使得SSE增量最小的两个簇。

在本节，我们将重点关注基于全连接方法的凝聚层次聚类，其迭代过程可总结如下：

1）计算得到所有样本间的距离矩阵。

2）将每个数据点看作是一个单独的簇。

3）基于最不相似（距离最远）样本的距离，合并两个最接近的簇。

4）更新相似矩阵（样本间距离矩阵）。

5）重复步骤2到4，直到所有样本都合并到一个簇为止。

现在我们来讨论一下如何计算距离矩阵（步骤1）。在此之前，需要先随机生成一些样本数据用于计算。其中行代表不同的样本（ID值从0到4），列代表样本的不同特征（X，Y，Z）。

执行上述代码后，可以得到如下距离矩阵：

11.2.1　基于距离矩阵进行层次聚类

我们使用SciPy中spatial.distanct子模块下的pdist函数来计算距离矩阵，此矩阵作为层次聚类算法的输入：

在上述代码中，我们基于样本的特征X、Y和Z，使用欧几里得距离计算了样本间的两两距离。通过将pdist函数的返回值输入到squareform函数中，我们得到了一个记录成对样本间距离的对称矩阵：

下面我们使用SciPy中cluster.hierarchy子模块下的linkage函数，此函数以全连接作为距离判定标准，它能够返回一个所谓的关联矩阵（linkage matrix）。

不过在调用linkage函数之前，我们先仔细研究下此函数相关的文档信息：

从对函数的描述中可知：我们可以将由pdist函数得到的稠密矩阵（上三角）作为输入项。或者，将初始化的欧几里得距离矩阵（将矩阵参数项的值设定为euclidean）作为linkage的输入。不过，我们不应使用前面提及的用squareform函数得到的距离矩阵，因为这会生成与预期不同的距离值。综合来讲，这里可能出现三种不同的情况：

·错误的方法：在本方法中，我们使用了通过squareform函数得到的距离矩阵，代码如下：

·正确的方法：在本方法中，我们使用了稠密距离矩阵，代码如下：

·正确的方法：在本方法中，我们以矩阵格式的示例数据作为输入，代码如下：

为了更进一步分析聚类结果，我们通过下面的方式将数据转换为pandas的DataFrame格式（最好在IPython Notebook中使用）：

如下表所示，关联矩阵包含多行，每行代表一次簇的合并。矩阵的第一列和第二列分别表示每个簇中最不相似（距离最远）的样本，第三列为这些样本间的距离，最后一列为每个簇中样本的数量。

现在我们已经完成了关联矩阵的计算，下面采用树状图的形式对聚类结果进行可视化展示：

如果是通过执行上述代码生成的图像，或者阅读本书的电子版本，会发现树状图的分支使用了不同的颜色。着色方案来自matplotlib的一个色彩列表，它基于树状图中的距离阈值循环生成不同颜色。例如，通过删除上述代码中的相关注释符，就可使用黑色来绘制此树状图。

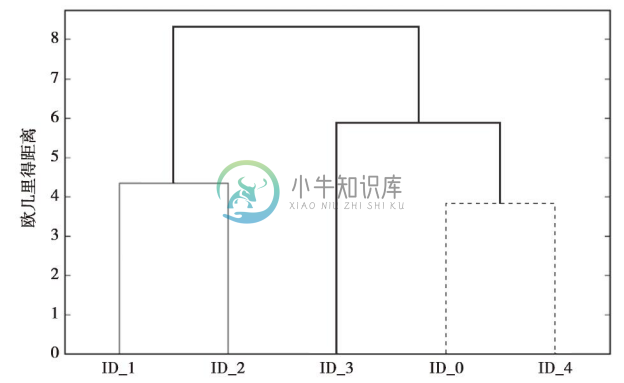
此树状图描述了采用凝聚层次聚类合并生成不同簇的过程。例如，从图中可见，首先是ID_0和ID_4合并，接下来是ID_1和ID_2合并，也就是基于欧几里德距离矩阵，选择最不相似的样本进行合并。

11.2.2　树状图与热度图的关联

在实际应用中，层次聚类的树状图通常与热度图（heat map）结合使用，这样我们可以使用不同的颜色来代表样本矩阵中的独立值。在本节中，我们讨论如何将树状图附加到热度图上，并同时显示在一行上。

不过，将树状图与热度图结合还是需要一点小技巧的，我们将逐步介绍这一步骤：

1）创建一个figure对象，并通过add_axes属性来设定x轴位置、y轴位置，以及树状图的宽度和高度。此外，我们沿逆时针方向将树状图旋转90度，代码如下：

2）接下来，我们根据树状图对象中的簇类标重排初始化数据框（DataFrame）对象中的数据，它本质上是一个Python字典，可通过leaves键访问得到，代码如下：

3）基于重排后的数据框（DataFrame）数据，在树状图的右侧绘制热度图：

4）最后，为了美化效果，我们删除了坐标轴标记，并将坐标轴的刻度隐藏。此外，我们还加入了色条，并分别在x和y轴上显示特征名和样本ID名称。代码如下：

通过上述步骤，便可看到热度图和树状图并列显示的图像：

如上图所示，热度图中的行反映了树状图中样本聚类的情况。除了简单的树状图外，热度图中用颜色代表的各样本及其特征为我们提供了关于数据集的一个良好的概括。

11.2.3　通过scikit-learn进行凝聚聚类

在本节中，我们将使用scikit-learn进行基于凝聚的层次聚类。不过，scikit-learn中已经实现了一个AgglomerativeClustering类，它允许我们选择待返回簇的数量。当我们想要对层次聚类树进行剪枝时，这个功能是非常有用的。将参数n_cluster的值设定为2，我们可以采用与前面相同的完全连接方法，基于欧几里得距离矩阵，将样本划分为两个簇：

通过对簇类标的预测结果进行分析，我们可以看出：第一、第四、第五个（ID_0，ID_3和ID_4）样本被划分至第一个簇（0），样本ID_1和ID_2被划分至第二个簇（1），这与此前通过树状图得到的结果一致。