10.5 线性回归模型性能的评估

在前面的小节中，我们讨论了如何在训练数据上拟合回归模型。然而，通过前面章节的学习，我们了解到：为了获得对模型性能的无偏估计，在训练过程中使用未知数据对模型进行测试是至关重要的。

还记得在第6章中，将数据集划分为训练数据集和测试数据集，前者用于模型的拟合，后者用于评估模型在未知数据上的泛化性能。简单回归模型的介绍就到这里，我们现在使用数据集中的所有变量训练多元回归模型：

这个模型使用了多个解释变量，我们无法在二维图上绘制线性回归曲线（更确切地说是超平面），不过可以绘制出预测值的残差（真实值与预测值之间的差异或者垂直距离）图，从而对回归模型进行评估。残差图作为常用的图形分析方法，可对回归模型进行评估、获取模型的异常值，同时还可检查模型是否是线性的，以及误差是否随机分布。

使用如下代码，我们绘制得到残差图，其中，通过将预测结果减去对应目标变量真实值，便可获得残差的值：

执行上述代码，我们应该看到如下残差图像，其中包含一条穿过x轴原点的直线，如下图所示：

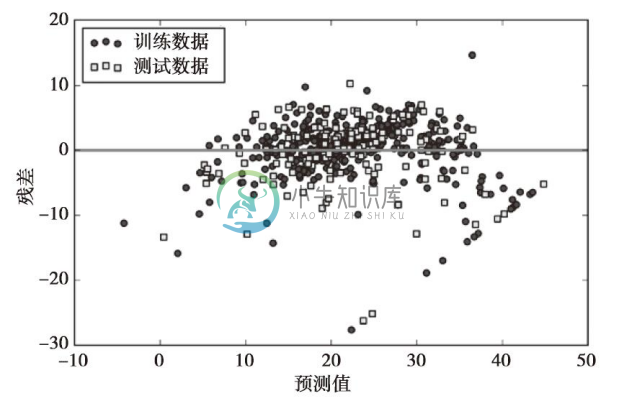
完美的预测结果其残差应为0，但在实际应用中，这种情况可能永远都不会发生。不过，对于一个好的回归模型，我们期望误差是随机分布的，同时残差也随机分布于中心线附近。如果我们从残差图中找出规律，这意味着模型遗漏了某些能够影响残差的解释信息，就如同刚看到的残差图那样，其中有着些许规律。此外，我们还可以使用残差图来发现异常值，这些异常值点看上去距离中心线有较大的偏差。

另外一种对模型性能进行定量评估的方法称为均方误差（Mean Squared Error，MSE），它是线性回归模型拟合过程中，最小化误差平方和（SSE）代价函数的平均值。MSE可用于不同回归模型的比较，或是通过网格搜索进行参数调优，以及交叉验证等：

执行如下代码：

可以看到，训练集上的MSE值为19.96，而测试集上的MSE值骤升为27.20，这意味着我们的模型过拟合于训练数据。

某些情况下决定系数（coefficient of determination）（R²）显得尤为有用，它可以看作是MSE的标准化版本，用于更好地解释模型的性能。换句话说，R²是模型捕获的响应方差的分数。R²值的定义如下：

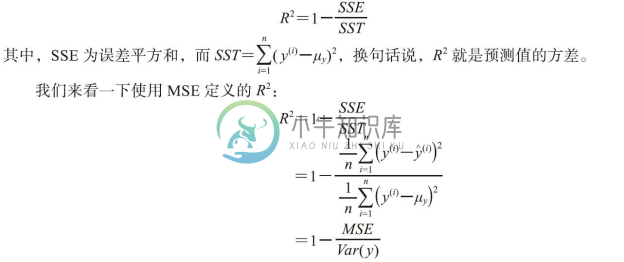
对于训练数据集来说，R²的取值范围介于区间[0,1]，对于测试集来说，其值可能为负。如果R²＝1，此时MSE＝0，这意味着模型完美拟合了数据。

在训练集上进行评估，R²的值为0.765，看起来还不错。不过，在测试上R²的值仅为0.673，计算代码如下：