线性回归

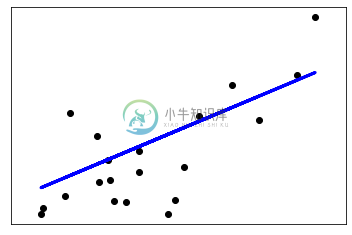
本例仅使用糖尿病数据集的第一个特征，来展示线性回归在二维空间上的表现。下图中的直线, 即是线性回归所确定的一个界限，其目标是使得数据集中的实际值与线性回归所得的预测值之间的残差平方和最小。

同时也计算了回归系数、残差平方和以及解释方差得分，来判断该线性回归模型的质量。

原文解释和代码不符合:

实际上计算了回归系数, 均方误差（MSE）,判定系数(r2_score)

判定系数和解释方差得分并不绝对相等，当实际值和预测值之间的误差均值为0时，两者相同，否则数值上有着略微误差。均方误差和残差平方和虽然都是定义预测值和实际值的偏离关系，但是数值大小的差距较大。

解释方差得分函数: explained_variance_score()。

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score, explained_variance_score

# 加载糖尿病数据集
diabetes = datasets.load_diabetes()

# 只使用1个特征
diabetes_X = diabetes.data[:, np.newaxis, 2]

# 划分训练,测试集
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]

# 创建线性回归模型
regr = linear_model.LinearRegression()

# 训练这个模型
regr.fit(diabetes_X_train, diabetes_y_train)

# 使用模型做预测
diabetes_y_pred = regr.predict(diabetes_X_test)

# 评价预测结果
print('回归系数(coef_):', regr.coef_)
print("均方误差(MSE): %.2f"% mean_squared_error(diabetes_y_test, diabetes_y_pred))
print('判断系数(r2_score): %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
# 额外增加
print('解释方差得分(explained_variance_score): %.2f' % explained_variance_score(diabetes_y_test, diabetes_y_pred))

回归系数(coef_): [938.23786125]
均方误差(MSE): 2548.07
判断系数(r2_score): 0.47
解释方差得分(explained_variance_score): 0.53

# 绘制输出
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)

plt.xticks(())
plt.yticks(())

plt.show()