2.4. 双聚类
校验者: @udy 翻译者: @程威
Biclustering 可以使用 sklearn.cluster.bicluster 模块。 Biclustering 算法对数据矩阵的行列同时进行聚类。 同时对行列进行聚类称之为 biclusters。 每一次聚类都会通过原始数据矩阵的一些属性确定一个子矩阵。
例如, 一个矩阵 (10, 10) , 一个 bicluster 聚类,有三列二行,就是一个子矩阵 (3, 2)
>>> import numpy as np
>>> data = np.arange(100).reshape(10, 10)
>>> rows = np.array([0, 2, 3])[:, np.newaxis]
>>> columns = np.array([1, 2])
>>> data[rows, columns]
array([[ 1, 2],
[21, 22],
[31, 32]])
为了可视化, 给定一个 bicluster 聚类,数据矩阵的行列可以重新分配,使得 bi-cluster 是连续的。
算法在如何定义 bicluster 方面有一些不同,常见类型包括:
- 不变的 values , 不变的 rows, 或者不变的 columns。
- 异常高的或者低的值。
- 低方差的子矩阵。
- 相关的 rows 或者 columns。
算法在分配给 bicluster 行列的方式不同, 会导致不同的 bicluster 结构。 当行和列分成分区时,会发生对角线或者棋盘结构。
如果每一行和每一列同属于一种 bicluster ,就重新排列数据矩阵的行和列,会使得 bicluster 呈现对角线。 下面是一个例子,此结构的biclusters 具有比其他行列更高的平均值:
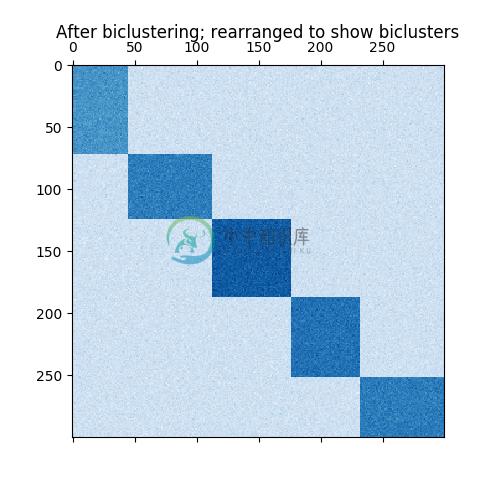
在棋盘结构的例子中, 每一行属于所有的列类别, 每一列属于所有的行类别。 下面是一个例子,每个 bicluster 中的值差异较小:
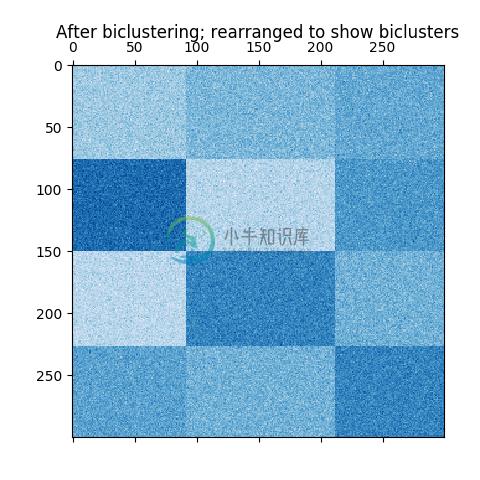
在拟合模型之后, 可以在 rows_ 和 columns_ 属性中找到行列 cluster membership 。 rows_[i] 是一个二进制的向量, 就是属于 bicluster i 的一行。 同样的, columns_[i] 就表示属于 bicluster i 的列。
一些模块也有 row_labels_ 何 column_labels_ 属性。 这些模块对行列进行分区, 例如对角线或者棋盘 bicluster 结构。
Note
Biclustering 在不同的领域有很多其他名称,包括 co-clustering, two-mode clustering, two-way clustering, block clustering, coupled two-way clustering 等.有一些算法的名称,比如 Spectral Co-Clustering algorithm, 反应了这些备用名称。
2.4.1. Spectral Co-Clustering
SpectralCoclustering算法找到的 bicluster 的值比相应的其他行和列更高。
每一个行和列都只属于一个 bicluster, 所以重新分配行和列,使得分区连续显示对角线上的 high value:
Note
算法将输入的数据矩阵看做成二分图:该矩阵的行和列对应于两组顶点,每个条目对应于行和列之间的边,该算法近似的进行归一化,对图进行切割,找到更重的子图。
2.4.1.1. 数学公式
找到最优归一化剪切的近似解,可以通过图形的 Laplacian 的广义特征值分解。 通常这意味着直接使用 Laplacian 矩阵. 如果原始数据矩阵 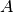 有形状
有形状 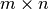 , 则对应的 bipartite 图的 Laplacian 矩阵具有形状
, 则对应的 bipartite 图的 Laplacian 矩阵具有形状 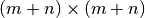 。 但是, 在这种情况直接使用
。 但是, 在这种情况直接使用 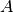 , 因为它更小,更有作用。
, 因为它更小,更有作用。
输入矩阵 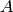 被预处理如下:
被预处理如下:
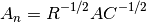
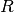 是
是 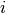 对角线矩阵,和
对角线矩阵,和 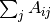 相同,
相同, 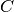 是
是 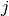 的对角吸纳矩阵,等同于
的对角吸纳矩阵,等同于 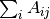 。
。
奇异值分解, 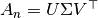 , 提供了
, 提供了 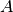 行列的分区. 左边的奇异值向量给予行分区,右边的奇异值向量给予列分区。
行列的分区. 左边的奇异值向量给予行分区,右边的奇异值向量给予列分区。
 奇异值向量从第二个开始, 提供所需的分区信息。 这些用于形成矩阵 :<cite>Z</cite>:
奇异值向量从第二个开始, 提供所需的分区信息。 这些用于形成矩阵 :<cite>Z</cite>:

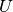 的列是
的列是 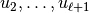 , 和
, 和 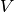 相似 。
相似 。
然后 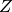 的 rows 通过使用 k-means 进行聚类.
的 rows 通过使用 k-means 进行聚类. n_rows 标签提供行分区, 剩下的 n_columns 标签 提供 列分区。
例子:
- A demo of the Spectral Co-Clustering algorithm: 如何用 bicluster 数据矩阵并应用。
- Biclustering documents with the Spectral Co-clustering algorithm:一个在 20 个新闻组数据集中发现 biclusters 的例子
参考文献:
- Dhillon, Inderjit S, 2001. Co-clustering documents and words using bipartite spectral graph partitioning.
2.4.2. Spectral Biclustering
SpectralBiclustering算法假设输入的数据矩阵具有隐藏的棋盘结构。 具有这种结构的矩阵的行列 可能被分区,使得在笛卡尔积中的 大部分 biclusters 的 row clusters 和 column cluster 是近似恒定的。
例如,如果有两个row 分区和三个列分区,每一行属于三个 bicluster ,每一列属于两个 bicluster。
这个算法划分矩阵的行和列,以至于提供一个相应的块状不变的棋盘矩阵,近似于原始矩阵。
2.4.2.1. 数学表示
输入矩阵  先归一化,使得棋盘模式更明显。有三种方法:
先归一化,使得棋盘模式更明显。有三种方法:
- 独立的行和列归一化, as in Spectral Co-Clustering. 这个方法使得行和一个常数相加,列和变量相加。
- Bistochastization: 重复行和列归一化直到收敛。该方法使得行和列都相加
相同的常数。
- Log 归一化: 计算数据矩阵的对数
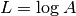 . 列就是
. 列就是 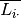 , 行就是
, 行就是 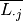 , 总体上来看
, 总体上来看 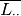 of
of 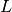 被计算的. 最后矩阵通过下面的公式计算
被计算的. 最后矩阵通过下面的公式计算

归一化后,首先少量的奇异值向量被计算,只是在 Spectral Co-Clustering 算法中。
如果使用 log 归一化,则所有的奇异向量都是有意义的。但是, 如果是独立的归一化或双曲线化 被使用,第一个奇异矢量, 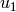 和
和 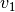 。 会被丢弃。 从现在开始, “first” 奇异值向量与
。 会被丢弃。 从现在开始, “first” 奇异值向量与 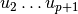 和
和 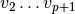 相关,除了日志归一化的情况。
相关,除了日志归一化的情况。
给定这些奇异值向量, 将他们排序,通过分段常数向量保证最佳近似。 使用一维 k-means 找到每个向量的近似值 并使用欧几里得距离得分。 Some subset of 最好的左右奇异值向量的子集被选择。 下一步, 数据预计到这个最佳子集的奇异向量和聚类。
例如,如果 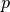 奇异值向量被计算,最好按照描述找到
奇异值向量被计算,最好按照描述找到 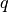 , 其中 <img src="https://www.xnip.cn/wp-content/uploads/2020/docimg4/cc9d324e8bc61a67cc1947f73bf5b618.jpg" alt="q
, 其中 <img src="https://www.xnip.cn/wp-content/uploads/2020/docimg4/cc9d324e8bc61a67cc1947f73bf5b618.jpg" alt="q
。 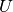 列为,the
列为,the 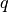 最佳左奇异向量的矩阵, 并且
最佳左奇异向量的矩阵, 并且 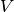 对于右边是类似的. 要划分行, 将
对于右边是类似的. 要划分行, 将 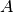 的 投影到
的 投影到 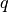 维空间:
维空间: 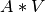 。
。 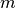 行
行 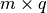 矩阵的行作为采样和使用 k-means 的聚类处理产生行标签。 类似地,将列投影到
矩阵的行作为采样和使用 k-means 的聚类处理产生行标签。 类似地,将列投影到 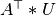 ,并且对
,并且对 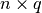 矩阵进行聚类得到列标签。
矩阵进行聚类得到列标签。
示例:
- A demo of the Spectral Biclustering algorithm: 一个简单的例子 显示如何生成棋盘矩阵和 bicluster
.
参考文献:
- Kluger, Yuval, et. al., 2003. Spectral biclustering of microarray data: coclustering genes and conditions.
2.4.3. Biclustering 评测
有两种评估双组分结果的方法:内部和外部。 诸如群集稳定性等内部措施只依赖于数据和结果本身。 目前在scikit-learn中没有内部的二集群措施。外部措施是指外部信息来源,例如真正的解决方案。 当使用真实数据时,真正的解决方案通常是未知的,但是,由于真正的解决方案是已知的,因此人造数据的双重分析可能对于评估算法非常有用。
为了将一组已发现的双组分与一组真正的双组分进行比较, 需要两个相似性度量:单个双色团体的相似性度量,以及将这些个体相似度结合到总分中的方法。
为了比较单个双核,已经采用了几种措施。现在,只有Jaccard索引被实现:
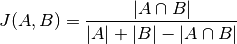
和 是 biclusters, 是交叉点的元素的数量。
Jaccard 索引 达到最小值0,当 biclusters 不重叠的时候,并且当他们相同干的时候,最大值为1。
有些方法已经开发出来,用来比较两个 biclusters 的数据集。 从现在开始 之后 consensus_score (Hochreiter et. al., 2010) 是可以用:
- 使用 Jaccard 索引或类似措施,计算 biclusters 的 bicluster 相似性。
- 以一对一的方式将 bicluster 分从一组分配给另一组,以最大化其相似性的总和。该步骤使用匈牙利算法执行。
- 相似性的最终总和除以较大集合的大小。
最小共识得分为0,发生在所有 biclusters 完全不相似时。当两组 biclusters 相同时,最大分数为1。
参考文献:
- Hochreiter, Bodenhofer, et. al., 2010. FABIA: factor analysis for bicluster acquisition.

