用 scikit-learn 求解多项式回归问题
优质
小牛编辑
144浏览
2023-12-01

住房价格样本
样本 面积(平方米) 价格(万元)
| 样本 | 面积(平方米) | 价格(万元) |
| 1 | 50 | 150 |
| 2 | 100 | 200 |
| 3 | 150 | 250 |
| 4 | 200 | 280 |
| 5 | 250 | 310 |
| 6 | 300 | 330 |
做图像
# coding:utf-8
import sys
reload(sys)
sys.setdefaultencoding( "utf-8" )
import matplotlib.pyplot as plt
import numpy as np
plt.figure() # 实例化作图变量
plt.title('single variable') # 图像标题
plt.xlabel('x') # x轴文本
plt.ylabel('y') # y轴文本
plt.axis([30, 400, 100, 400])
plt.grid(True) # 是否绘制网格线
xx = [[50],[100],[150],[200],[250],[300]]
yy = [[150],[200],[250],[280],[310],[330]]
plt.plot(xx, yy, 'k.')
plt.show() # 展示图像用线性回归
在上述代码中加上
model = LinearRegression()
model.fit(xx, yy)
x2 = [[30], [400]]
y2 = model.predict(x2)
plt.plot(x2, y2, 'g-')得到回归图像:
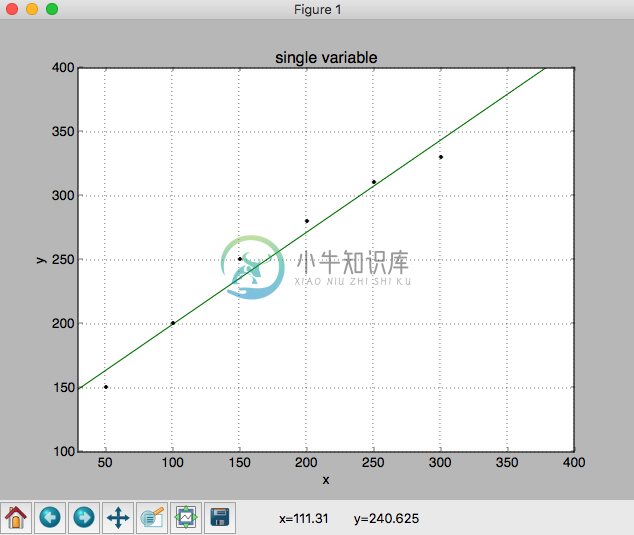
但是实际情况是,如果房屋面积一味的增加,房价并不会线性增长,因此线性关系已经无法描述真实的房价问题
采用多项式回归
首先我们用二次多项式
# coding:utf-8
import sys
reload(sys)
sys.setdefaultencoding( "utf-8" )
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
plt.figure() # 实例化作图变量
plt.title('single variable') # 图像标题
plt.xlabel('x') # x轴文本
plt.ylabel('y') # y轴文本
plt.axis([30, 400, 100, 400])
plt.grid(True) # 是否绘制网格线
X = [[50],[100],[150],[200],[250],[300]]
y = [[150],[200],[250],[280],[310],[330]]
X_test = [[250],[300]] # 用来做最终效果测试
y_test = [[310],[330]] # 用来做最终效果测试
plt.plot(X, y, 'k.')
model = LinearRegression()
model.fit(X, y)
X2 = [[30], [400]]
y2 = model.predict(X2)
plt.plot(X2, y2, 'g-')
xx = np.linspace(30, 400, 100) # 设计x轴一系列点作为画图的x点集
quadratic_featurizer = PolynomialFeatures(degree=2) # 实例化一个二次多项式特征实例
X_train_quadratic = quadratic_featurizer.fit_transform(X) # 用二次多项式对样本X值做变换
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1)) # 把训练好X值的多项式特征实例应用到一系列点上,形成矩阵
regressor_quadratic = LinearRegression() # 创建一个线性回归实例
regressor_quadratic.fit(X_train_quadratic, y) # 以多项式变换后的x值为输入,代入线性回归模型做训练
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-') # 用训练好的模型作图
print '一元线性回归 r-squared', model.score(X_test, y_test)
X_test_quadratic = quadratic_featurizer.transform(X_test)
print '二次回归 r-squared', regressor_quadratic.score(X_test_quadratic, y_test)
plt.show() # 展示图像作图如下:

红色为二次多项式回归图像,可以看到比线性模型吻合度高,输出的R方结果为:
一元线性回归 r-squared 0.0755555555556
二次回归 r-squared 0.999336734694可以看到二次回归效果更好
我们继续尝试一下三次回归
增加如下代码:
cubic_featurizer = PolynomialFeatures(degree=3)
X_train_cubic = cubic_featurizer.fit_transform(X)
regressor_cubic = LinearRegression()
regressor_cubic.fit(X_train_cubic, y)
xx_cubic = cubic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_cubic.predict(xx_cubic))
X_test_cubic = cubic_featurizer.transform(X_test)
print '三次回归 r-squared', regressor_cubic.score(X_test_cubic, y_test)图像如下:

R方输出如下:
一元线性回归 r-squared 0.0755555555556
二次回归 r-squared 0.999336734694
三次回归 r-squared 0.999464600659可以看到三次回归比二次回归效果又好了一些,但是不是很明显。所以二次回归更可能是最适合的回归模型,三次回归可能有过拟合现象


