看数据科学家是如何找回丢失的数据的（二）

优质

小牛编辑

124浏览

2023-12-01

连续型变量是如何做数据填补的

上一节中讲的Embarked的填补是一种离散型变量的填补方式，也就是通过统计规律来预测。那么对于连续型变量如果使用这种方法就不合适了，而应该使用某一种插值方式。比如Age这种数据，根据统计规律，假设其他人年龄多数是50岁，其他人都小于50岁，那么就预测是50岁吗？显然不对，而应该是小于50的某个值。那么如何根据统计规律来计算插值呢？我们来介绍一下mice

mice就是链式方程多元插值(Multivariate Imputation by Chained Equations)的简写

mice包可以对缺失数据的模式做一个很好的理解，为了说明这个事情，我们依然使用泰坦尼克数据集（不了解请见《十八-R语言特征工程实战》）

首先我们选择一些我们想要观察的列：

> full1 <- cbind(PassengerId=full$PassengerId,Pclass=full$Pclass,Sex=full$Sex,Age=full$Age,Fare=full$Fare,Embarked=full$Embarked,Title=full$Title,Fsize=full$Fsize)

然后我们利用mice查看一下数据缺失的模式：

> library(mice)
> md.pattern(full1)
     PassengerId Pclass Sex Embarked Title Fsize Fare Age
1045           1      1   1        1     1     1    1   1   0
 263           1      1   1        1     1     1    1   0   1
   1           1      1   1        1     1     1    0   1   1
               0      0   0        0     0     0    1 263 264

从上面可以方便的看出一共有1045个样本字段完整，263个样本缺失Age，1个样本缺失Fare

我们还可以通过VIM来图形化的展示数据缺失情况：

> library(VIM)
> aggr_plot <- aggr(full1, col = c('navyblue', 'red'), numbers=TRUE, sortVars=TRUE,labels=names(full1), cex.axis=.7, gap=3,ylab=c("Histogram of missing data", "Pattern"))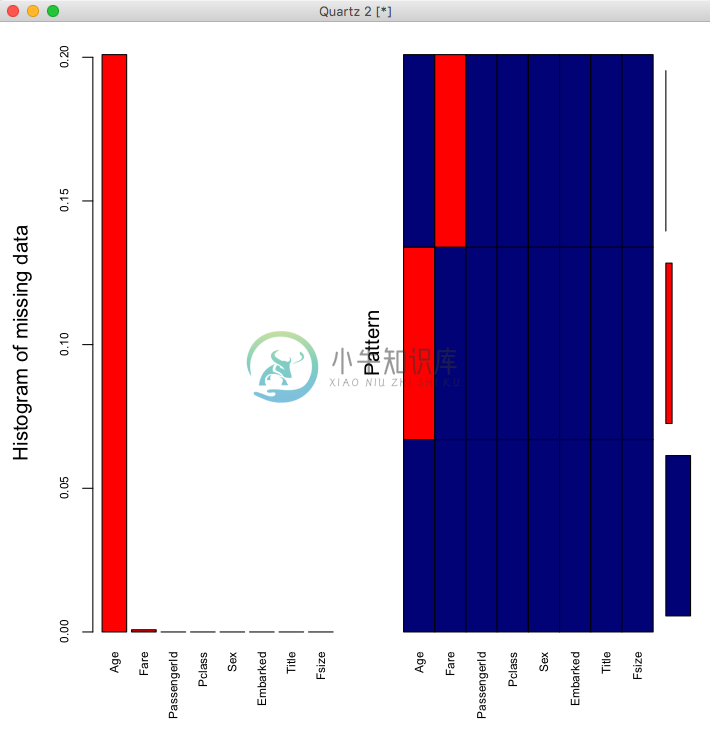

从图中可以看出Age缺失最多(20%左右)，其次是Fare(比例很小)

下面我们利用mice的数据填补方法来填补，我们选用随机森林模型(rf)，如下：

> set.seed(129)
> mice_mod <- mice(full[, !names(full) %in% c('PassengerId','Name','Ticket','Cabin','Family','Surname','Survived')], method='rf')

经过随机森林模型迭代训练，生成了mice_mod这个模型，下面我们生成完整数据并取出来，这里面实际包含了多个完整的副本，每个副本都对缺失值做了插补不同的值，complete默认会取出其中一个

> mice_output <- complete(mice_mod)

这里生成的mice_output就是在full基础上填充了缺失值的数据

为了观察新旧数据分布是否有过大的变化，我们画出分布直方图如下：

> par(mfrow=c(1,2))
> hist(full$Age, freq=F, main='Age: Original Data',
+   col='darkgreen', ylim=c(0,0.04))
> hist(mice_output$Age, freq=F, main='Age: MICE Output',
+   col='lightgreen', ylim=c(0,0.04))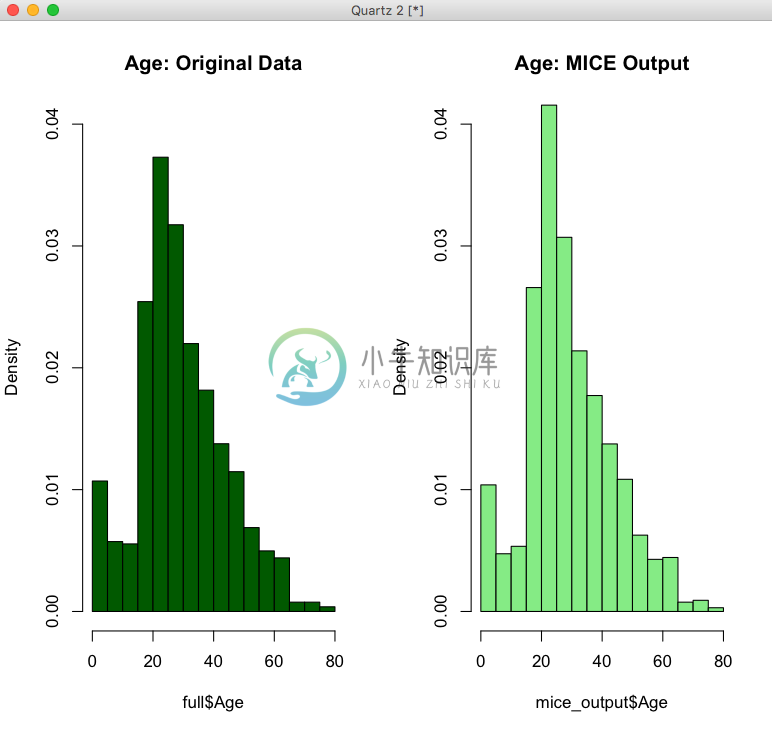

讲解一下：这里的par(mfrow=c(1,2))指的是准备一张一行两列的画布，这样可以把两个直方图画在一起，freq=F这里的F是False，表示展示的列不是频次而是比例，ylim=c(0,0.04)是y轴的取值范围

我们也可以通过直观的看填补值的散点图来看是否合理：

> library(lattice)
> xyplot(mice_mod,Fare ~ Age,pch=18,cex=1)

xyplot的第一个参数是mice训练出的模型数据，第二个参数Fare ~ Age指明了x轴是Age，y轴是Fare，图中洋红色的点是自动填补的，看起来还是比较符合分布情况的，在这里，我们主要看的是y轴填补数据情况，如果想看Age的填补情况则把两个属性调过来，如下：

> xyplot(mice_mod,Age ~ Fare,pch=18,cex=1)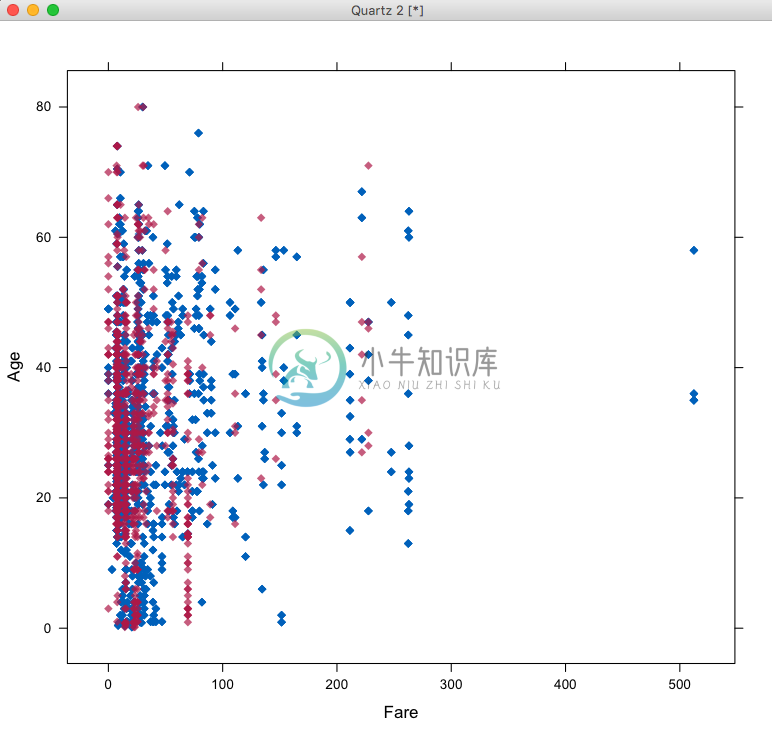

我们还可以画出密度图：

> densityplot(mice_mod)

从图中可以看出洋红色表示填补的数据集的分布密度情况，蓝色是原始数据的分布密度，如果填补效果较好，分布应该相似

上面我们说到mice实际上返回了多个完整数据副本，每个副本插的值都不同，那么我们还可以看下这些副本的插值情况：

> stripplot(mice_mod, pch = 20, cex = 1.2)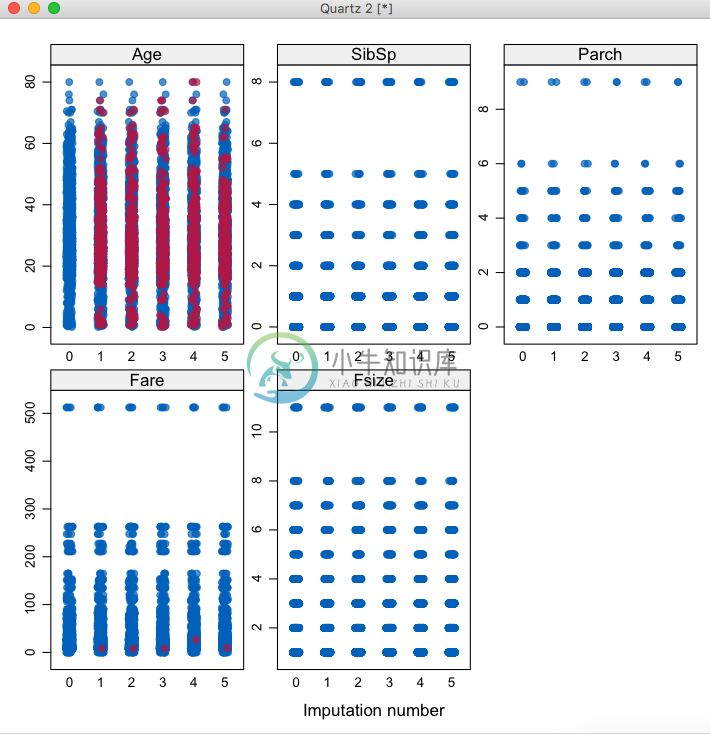

注意观察图中的Age和Fare两个图，每张图中都可以看到5种插值副本的分布情况

利用数据预测做数据填补

和上面的mice类似，也是建立一个模型来预测，但是不是采用插值的方式了，而是通过训练模型来预测数据，一般用来填补离散型变量的值，假设我们认为Fare是离散的值(因为票价一般是固定的几个价钱)，我们把和Fare有关的几个变量(乘客等级、家庭人员数目、登船港口)都作为特征来训练一棵决策树

> library("rpart")
> library("rpart.plot")
> my_tree <- rpart(Fare ~ Pclass + Fsize + Embarked, data = train, method = "class", control=rpart.control(cp=0.0001))
> prp(my_tree, type = 4, extra = 100)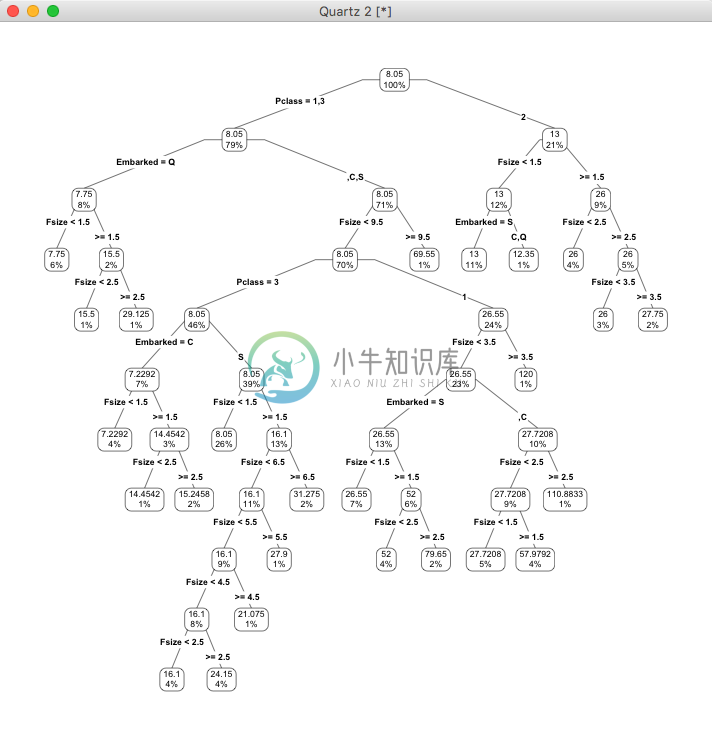

我们可以看到通过乘客等级、家庭人员数目、登船港口几个特征的训练，我们得出了一棵决策树，利用这棵决策树我们可以预测缺失值：

> full$PassengerId[is.na(full$Fare)]
[1] 1044

我们看到1044号乘客没有Fare，那么对他做预测

> predict(my_tree, full[1044,], type = "class")
1044
8.05
248 Levels: 0 4.0125 5 6.2375 6.4375 6.45 6.4958 6.75 6.8583 6.95 ... 512.3292

可以看出预测的结果是8.05