神经网络模型的原理
人工神经网络
人工神经网络又叫神经网络,是借鉴了生物神经网络的工作原理形成的一种数学模型。下面是一张生物神经元的图示:
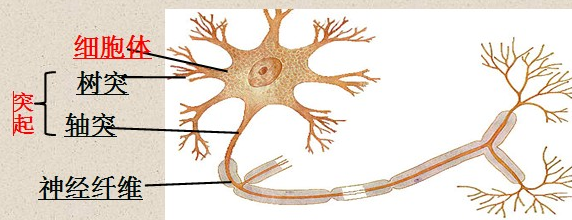
生物神经网络就是由大量神经元构成的网络结构如下图:

生物的神经网络是通过神经元、细胞、触电等结构组成的一个大型网络结构,用来帮助生物进行思考和行动等。那么人们就想到了电脑是不是也可以像人脑一样具有这种结构,这样是不是就可以思考了?
类似于神经元的结构,人工神经网络也是基于这样的神经元组成:
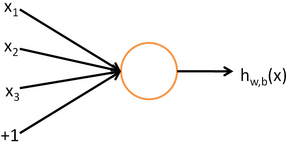
这里面的x1、x2、x3是输入值,中间的圆就像是神经元,经过它的计算得出hw,b(x)的结果作为神经元的输出值。
由这样的神经元组成的网络就是人工神经网络:
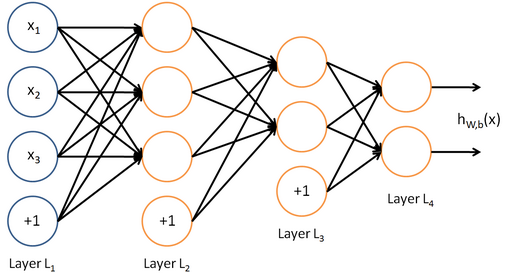
其中橙色的圆都是用来计算hw,b(x)的,纵向我们叫做层(Layer),每一层都以前一层为输入,输出的结果传递给下一层
这样的结构有什么特别的吗?
如果我们把神经网络看做一个黑盒,那么x1、x2、x3是这个黑盒的输入X,最右面的hw,b(x)是这个黑盒的输出Y,按照之前几篇机器学习的文章可以知道:这可以通过一个数学模型来拟合,通过大量训练数据来训练这个模型,之后就可以预估新的样本X应该得出什么样的Y
但是使用普通的机器学习算法训练出的模型一般都比较肤浅,就像是生物的进化过程,如果告诉你很久以前地球上只有三叶虫,现在地球上有各种各样的生物,你能用简单的模型来表示由三叶虫到人类的进化过程吗?不能。但是如果模拟出中间已知的多层隐藏的阶段(低等原始生物、无脊椎动物、脊椎动物、鱼类、两栖类、爬行动物、哺乳动物、人类时代)就可以通过海量的训练数据模拟出
也可以类比成md5算法的实现,给你无数个输入字符串和它的md5值,你能用肤浅的算法推出md5的算法吗?不能。因为md5的计算是一阶段一阶段的,后一阶段的输入依赖前一阶段的结果,无法逆推。但是如果已知中间几个阶段,只是不知道这几个阶段的参数,那么可以通过海量数据训练出来。
以上说明了神经网络结构的特别之处:通过较深的多个层次来模拟真实情况,从而构造出最能表达真实世界的模型,它的成本就是海量的训练数据和巨大的计算量。
神经网络模型的数学原理
每一个神经元的数学模型是:
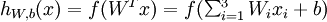
其中的矩阵向量乘法
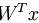
表示的就是输入多个数据的加权求和,这里的b(也就是上面图中的+1)是截距值,用来约束参数值,就像是一个向量(1,2,3)可以写成(2,4,6)也可以写成(10,20,30),那么我们必须取定一个值,有了截距值就可以限定了
其中f叫做激活函数,激活函数的设计有如下要求:1)保证后期计算量尽量小;2)固定取值范围;3)满足某个合理的分布。常用的激活函数是sigmond函数和双曲正切函数(tanh):
sigmond函数:
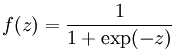
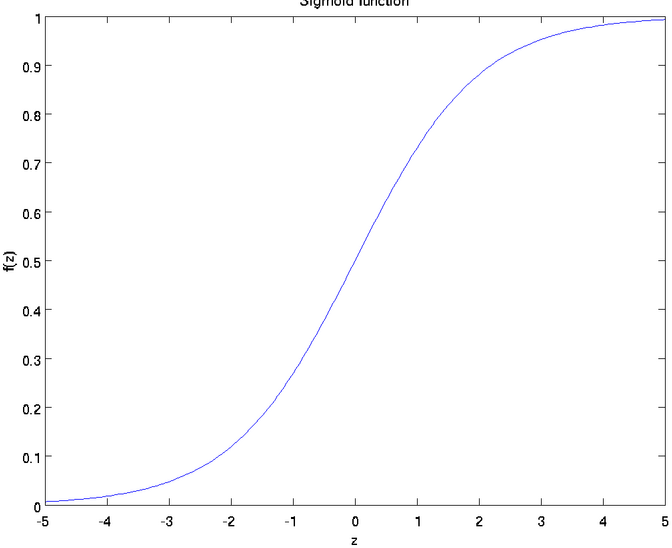
双曲正切函数(tanh):


这两个函数显然满足2)固定取值范围;3)满足某个合理的分布,那么对于1)保证后期计算量尽量小这个要求来说,他们的好处在于:
sigmond函数的导数是:

tanh函数的导数是:
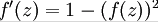
这会减少非常多的计算量,后面就知道了
当计算多层的神经网络时,对于如下三层神经网络来说
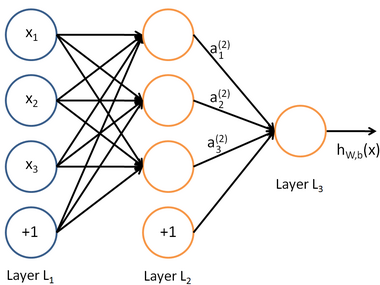
我们知道:
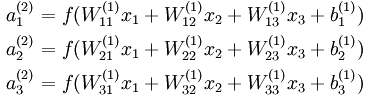
其中的

分别表示第2层神经元的输出的第1、2、3个神经元产生的值
这三个值经过第3层最后一个神经元计算后得出最终的输出是:

以上神经网络如果有更多层,那么计算原理相同
我们发现这些神经元的激活函数f是相同的,唯一不同的就是权重W,那么我们做学习训练的目标就是求解这里的W,那么我们如何通过训练获得更精确的W呢?
反向传导算法
回想一下前面文章讲过的回归模型,我们也是知道大量训练样本(x,y),未知的是参数W和b,那么我们计算W的方法是:先初始化一个不靠谱的W和b,然后用输入x和W和b预估y,然后根据预估的y和实际的y之间的差距来通过梯度下降法更新W和b,然后再继续下一轮迭代,最终逼近正确的W和b
神经网络算法也一样的道理,使用梯度下降法需要设计一个代价函数:
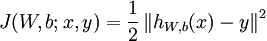
以上是对于一个(x,y)的代价函数,那么当我们训练很多个样本时:

其中m是样本数,左项是均方差,右项是规则化项,我们的目的就是经过多伦迭代让代价函数最小
我来单独解释一下我对这个规则化项的理解:规则化项的目的是防止过拟合,过拟合的含义就是“太适合这些样本了,导致不适合样本之外的数据,泛化能力低”,规则化项首先增大了代价函数的值,因为我们训练的目的是减小代价函数,所以我们自然就会经过多轮计算逐步减小规则化项,规则化项里面是各个W的平方和,因为∑W=1,所以要想平方和变小,只有让各个W的值尽量相同,这就需要做一个折中,也就是W既要显示出各项权重的不同,又要降低差别,因此这里的λ的值就比较关键了,λ大了权重就都一样了,小了就过拟合了,所以需要根据经验给一个合适的值。
具体计算过程
首先我们为W和b初始化一个很小的随机值,然后分别对每个样本经过上面说过的神经网络的计算方法,计算出y的预估值
然后按照梯度下降法对W和b进行更新:

这里面最关键的是偏导的计算方法,对于最终的输出节点来说,代价函数J(W,b)的计算方法比较简单,就是把输出节点的激活值和实际值之间的残差代入J(W,B)公式。而隐藏层里的节点的代价函数该怎么计算呢?
我们根据前向传导(根据输入x计算hW,b(x)的方法)算法来反推:
我们把第l层的第i个节点的残差记作:

因为hW,b(x)=f(Wx),这里面我们把Wx记作z,那么残差表达的其实是z的残差,也就是代价函数关于z的偏导
那么输出层的残差就是:

前一层的残差的推导公式为:

再往前的每一层都按照这个公式计算得出残差,这个过程就叫做反向传导算法
下面在回过头来看我们的更新算法
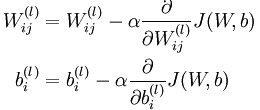
偏导数的求法如下:

说一下我对这个公式的理解:代价函数对W的偏导表达的是权重(第l层上第i个节点第j个输入)的变化,而这个变化就是一个误差值,误差体现在哪里呢?体现在它影响到的下一层节点的残差δ,那么它对这个残差的影响有多大呢,在于它的输出值a,所以得出这个偏导就是aδ。代价函数对b的偏导原理类似。
现在我们有了所有的a和δ,就可以更新所有的W了,完成了一轮迭代
大家已经注意到了,在计算δ的方法中用到了f'(z),这也就是激活函数的导数,现在明白为什么激活函数设计成sigmond或者tanh了吧?因为他们的导数更容易计算
总结一下整个计算过程
1. 初始化W和b为小随机数
2. 遍历所有样本,利用前向传导算法计算出神经网络的每一层输出a和最终的输出值hW,b(x)
3. 利用hW,b(x)和真实值y计算输出层的残差δ
4. 利用反向传导算法计算出所有层所有节点的残差δ
5. 利用每一层每一个节点的a和δ计算代价函数关于W和b的偏导
6. 用得出的偏导来更新权重
7. 返回2进行下一轮迭代直到代价函数不再收敛为止
8. 得到我们的神经网络
参考文献:UFLDL教程

