深究熵的概念和公式以及最大熵原理

熵

有关熵的介绍，我在《自己动手做聊天机器人 十五-一篇文章读懂拿了图灵奖和诺贝尔奖的概率图模型》中做过简单的介绍，熵的英文是entropy，本来是一个热力学术语，表示物质系统的混乱状态。

我们都知道信息熵计算公式是H(U)=-∑(p logp)，但是却不知道为什么，下面我们深入熵的本源来证明这个公式

假设下图是一个孤立的由3个分子构成一罐气体

那么这三个分子所处的位置有如下几种可能性：

图中不同颜色表示的是宏观状态(不区分每个分子的不同)，那么宏观状态一共有4种，而微观状态(每一种组合都是一种微观状态)一共有2^3=8种

再来看4个分子的情况

这时，宏观状态一共有5种，而微观状态一共有2^4=16种

事实上分子数目越多，微观数目会成指数型增长

这里面提到的宏观状态实际上就是熵的某一种表现，如果气体中各种宏观状态都有，那么熵就大，如果只存在一种宏观状态，那么熵就很小，如果把每个分子看做状态的形成元素，熵的计算就可以通过分子数目以某种参数求对数得到，这时我们已经了解了为什么熵公式中是对数关系

上面我们描述的一个系统(一罐气体)，假如我们有两罐气体，那么它们放在一起熵应该是可以相加的(就像上面由四种状态加了一个状态的一个分子变成5个状态)，即可加性，而微观状态是可以相乘的(每多一个分子，微观状态就会多出n-1种)，即相乘法则

综上，我们可以得出熵的计算公式是S=k ln Ω，其中k是一个常数，叫做玻尔兹曼常数，Ω是微观状态数，这个公式也满足了上面的可加性和相乘法则，即S1+S2=k ln (Ω1Ω2)

最大熵

在机器学习中我们总是运用最大熵原理来优化模型参数，那么什么样的熵是最大熵，为什么它就是最优的

这还是要从物理学的原理来说明，我们知道当没有外力的情况下气体是不断膨胀的而不会自动收缩，两个温度不同的物体接触时总是从高温物体向低温物体传导热量而不可逆。我们知道宏观状态越多熵越大，那么气体膨胀实际上是由较少的宏观状态向较多的宏观状态在变化，热传导也是一样，如此说来，一个孤立系统总是朝着熵增加的方向变化，熵越大越稳定，到最稳定时熵达到最大，这就是熵增原理

换句话说：熵是孤立系统的无序度的量度，平衡态时熵最大

将熵增原理也可以扩大到一切自发过程的普遍规律，比如如果你不收拾屋子，那么屋子一定会变得越来越乱而不会越来越干净整洁，扩大到统计学上来讲，屋子乱的概率更大，也就是说孤立系统中一切实际过程总是从概率小的状态向概率大的状态的转变过程，并且不可逆

信息熵

1948年，信息论之父香农发表的《通信的数学理论》中提出了“信息熵”的概念，从此信息熵对通信和计算机行业产生了巨大的影响。那么他到底说了些什么呢？

一个随机变量ξ有A1、A2、A3……共n个不同的结果，每个结果出现的概率是p1、p2、p3……，那么我们把ξ的不确定度定义为信息熵，参考上面物理学熵的定义，A1、A2、A3……可以理解为不同的微观状态，那么看起来信息熵应该是log n喽？不然，因为这个随机变量ξ一次只能取一个值而不是多个值，所以应该按概率把ξ劈开，劈成n份，每份的微观状态数分别是1/p1、1/p2、1/p3……，这样这n份的熵分别是log 1/p1、log 1/p2、log 1/p3……，再根据熵的可加性原理，得到整体随机变量ξ的信息熵是∑(p log 1/p)，即H(ξ) = -∑(p log p)

最大熵原理

继续看上面的信息熵公式，从公式可以看出，出现各种随机结果可能性越大，不确定性就越大，熵就越大。相反，如果只可能出现一种结果，那么熵就为0，因为这时p=1，-∑(p log p)=0

举个例子，投1000次硬币，最有可能的概率是正面1/2，负面1/2，因此熵是H(X) = -(0.5log0.5+0.5log0.5) = -0.5*math.log(2,1/2)*2 = -0.5*-1*2 = 1

那么假设只会出现正面，熵是H(X) = -1log1 = 0

实际上哪种是最符合实际情况的呢？显然是第一种，这就是最大熵模型的原理：在机器学习中之所以优化最大熵公式能训练出最接近正确值的参数值，是因为这是“最符合实际”的可能。换句有哲理的话说：熵越大越趋向于自然，越没有偏见

最大熵模型

机器学习中用到的最大熵模型是一个定义在条件概率分布P(Y|X)上的条件熵。其中X、Y分别对应着数据的输入和输出，根据最大熵原理，当熵最大时，模型最符合实际情况。那么这个条件熵应该是什么样的呢？

条件概率分布P(Y|X)上的条件熵可以理解为在X发生的前提下，Y发生所“新”带来的熵，表示为H(Y|X)，那么有

H(Y|X) = H(X,Y) - H(X)

其中H(X,Y)表示X、Y的联合熵，表示X、Y都发生时的熵，H(Y|X)的计算公式推导如下：

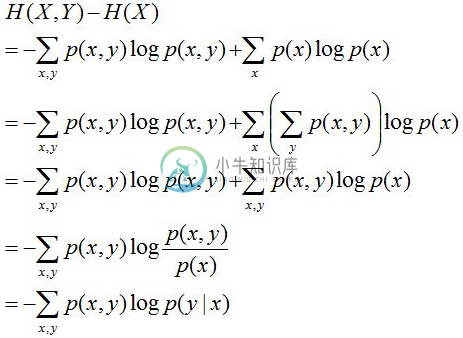
因此我们在机器学习中想方设法优化的就是这个东东，由于这里的p(x,y)无法统计，因此我们转成p(x)p(y|x)，这样得到公式如下：

H(Y|X) = -∑p(x)p(y|x)log p(y|x)

那么机器学习训练的过程实际就是求解p(y|x)的过程，其中p(x)可以通过x的最大似然估计直接求得

总结

至此，我们介绍完了熵的概念和公式以及最大熵原理和最大熵模型公式的由来，总之，熵来源于热力学，扩展于信息论，应用在机器学习领域，它表达的是一种无序状态，也是最趋向于自然、最符合实际的情况。为了更深入感受最大熵模型的魅力，后续我会把最大熵模型的应用不断渗透到机器学习教程的具体算法中