20. 连续分布的熵
离散概率集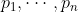 的熵已经定义为:
的熵已经定义为:
。
对于一个概率密度函数为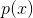 的连续分布,可以采用类似方式,将它的熵定义为:
的连续分布,可以采用类似方式,将它的熵定义为:
。
对于一个n维分布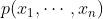 ,有:
,有:
。
如果有两个参数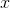 和
和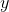 (它们本身可能是多维的),则
(它们本身可能是多维的),则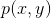 的联合熵和条件熵分别为:
的联合熵和条件熵分别为:
和
其中:
。
连续分布的熵具有离散分布的大多数性质(但不是全部性质)。具体来说,有:
如果
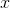 限定于其空间中的一个特定空间
限定于其空间中的一个特定空间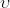 ,则
,则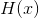 为最大值,当
为最大值,当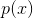 在其空间内为常数
在其空间内为常数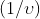 时,等于
时,等于。
对于任意两个变量
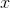 ,有:
,有:
当(且仅当)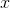 和
和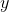 独立时,即
独立时,即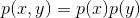 时(可能有一些概率为0的点除外),等式成立。
时(可能有一些概率为0的点除外),等式成立。考虑下面这种类型的广义求平均运算:
其中: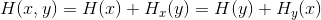
且。
设p(x)为一维分布。如果要求
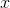 的标准差固定为
的标准差固定为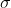 ,则当
,则当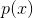 为高斯分布时的熵最大。为进行证明,必须以:
为高斯分布时的熵最大。为进行证明,必须以:
为约束条件,使: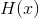
取最大值。根据变分法,这要求下式取最大值:。
其条件是:,
相应地(调整常数,以满足约束条件)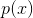 。
。
类似地,在n维中,假定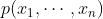 的二阶矩固定为
的二阶矩固定为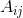 :
: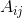 。
。
当是二阶矩为
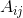 的
的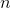 维高斯分布时,(通过类似计算)得到最大熵。
维高斯分布时,(通过类似计算)得到最大熵。标准差为
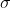 的一维高斯分布的熵由下式给出:
的一维高斯分布的熵由下式给出: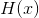 。
。
其计算如下:
类似的,具有相关形式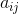 的
的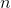 维高斯分布由下式给出:
维高斯分布由下式给出:
它的熵可以计算如下:
其中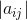 是元素为
是元素为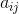 的行列式。
的行列式。如果
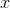 限制于半条线(对于
限制于半条线(对于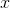 ,
,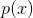 ),且
),且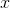 的一阶矩固定为a:
的一阶矩固定为a: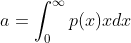 ,
,
则当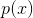
时,得到最大熵,且等于。
连续熵和离散熵之间有一个重要差别。在离散情况下,这个熵是以绝对方式度量随机变量的随机性。在连续情况下,这个度量是相对于坐标系统的。如果改变了坐标系,这个熵通常也会改变。事实上,如果我们将坐标系改为
,则新的熵为:
其中,是雅可比坐标变换。展开对数,并将变量变为
,得:
。
因此,新的熵等于原熵减去雅可比行列式的期望值。在连续情况下,可以将熵看作是一种相对于一种假定标准的随机性度量,这个“标准”就是选择坐标系,使每个小的体积分量具有给定权值。在改变坐标系时,新坐标系下的熵度量的是在新系统下,体积分量
具有相等权值时的随机性。
除了与坐标系具有这样依赖关系之外,熵的概念在连续情况下的重要性与离散情景中完全相同。这是因为,由此推导得出的信息率概念和信道容量概念取决于两个熵之差,这个差值与坐标系无关,当坐标系变化时,这两个熵的改变值相同。
连续分布的熵可能是负值。度量刻度设定一个任意零点,对应于单位体积上的一个均匀分布。如果一个分布的范围小于这一单位体积,它的熵会减小,从而为负值。但是,信息率和信道容量总是非负值。坐标系变化的一种特定情况为线性变换:
。
在这种情况下,雅可比变换行列式且
。
在坐标旋转情况下(或任何保测变换),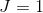 和
和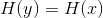 。
。

