12. 疑义度(equivocation)与信道容量
如果信道中存在噪声，一般情况下，无论对接收信号E执行什么处理，都无法确定地恢复出原始消息或发送信号。但是，有一些信息传送方式最适于对抗噪声。这就是我们现在要考虑的问题。
假定可能出现两个符号0和1，我们正在以每秒1000个符号的速率传送符号，其概率为
。因此，我们的信源正在以每秒1000比特的速率生成信息。在传输期间，噪声引入了误差，平均有百分之一的符号接收错误（发0收1，或发1收0）。信息的传送速率是多少呢？由于大约有1%的接收符号是错误的，所以信息传送速率当然小于1000比特/秒。我们的第一冲动可能会说：该速率为990比特/秒，就是减去误差的期望值。这一结果是不能令人满意的，因为它没有考虑到接收方并不知道这些误差会发生在哪里。我们可以将它延伸到一种极限情景，假定噪声是如此之大，接收到的符号完全与发送的信号无关。无论传送的是什么符号，收到1的概率总是
，收到0的情景也与此类似。因此，仅因为机缘巧合，大约有一半的接收符号是正确的，我们可能会说这个系统每秒传送500比特的信息，而实际上根本就没有传送任何信息。我们完全可以丢开这个信道，只需要在接收点抛掷硬币，就可以获得一个同样“出色”的传送过程。
显然，需要对发送信息量进行适当的修正，修正值就是接收信号中丢失的信息量，或者说，是当我们接收到实际发送内容的信号时存在的不确定性。在我们前面的讨论中，将熵作为不确定性的一种度量，在知道接收信号后，将消息的条件熵用作这一损失信息的度量看起来是合理的。后面将会看到，这实际上就是一个恰当的定义。根据这一思想，从生成速率（也就是信源的熵）中减去条件熵平均速率，就可以得到实际传送速率R。
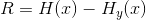
为方便起见，我们将条件熵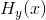
称为“疑义度”。它度量了接收信号的平均模糊度。
在上面考虑的示例中，如果收到0，则传送符号为0的后验概率为0.99，传送符号为1的后验概率为0.01。如果收到1，则这些数值颠倒过来。因此：
或者说81比特/秒。我们可以说，该系统是在以1000-81=919比特/秒的速率进行传送。在极端情况下，发送0时接收到0或1的概率相等，发送1时也是如此，则后验概率为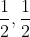
，则
或者说1000比特/秒。于是，传输速率为0，和实际情况一致。
下面的定义给出了疑义度的直观解读，还用于证明它作为惟一适当度量的正当性。我们考虑一个通信系统和一位观察者（或者辅助设施），这位观察者既能看到发送内容，又能看到接收内容（接收内容中包含因为噪声导致的错误）。这位观察者记下接收消息中的错误，并通过一个“校正信道”向接收端传送数据，使接收器能够纠正这些错误。这一情景在图8中示意给出。
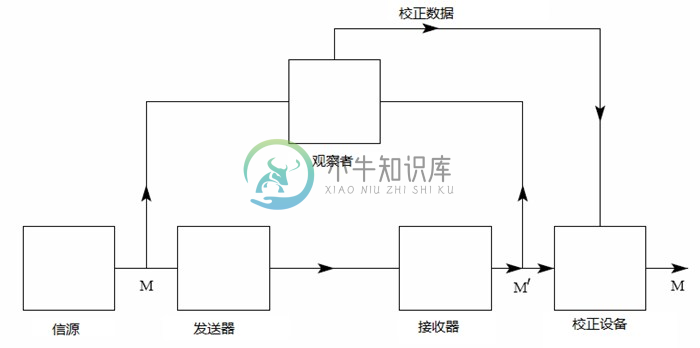
图8 校正系统的示意图
定理10：如果该校正信道的容量为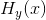
，则有可能对校正数据进行适当编码，以通过这一信道发送出去，除了任意小的一部分错误
之外，所有其他错误都可以被纠正。如果校正信道的容量小于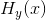
，则不可能实现。
大体来说，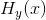
就是为了校正接收消息，在接收点每秒钟必须提供的附加信息量。
为了证明第一部分，考虑接收消息M'和相应原始消息M的长序列。以对数方式进行表示，有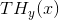
个M可以合理地生成每个M'。因此，每T秒中有
个二进制数位要传送。在容量为
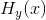的信道上，能够以
的错误频率来完成这一任务。
第二部分的证明如下：首先注意到对于任意离散随机变量x, y, z，
。
可以将左侧展开，得到：
如果我们把x看作信源的输出，y看作接收信号，z看作通过校正信道发送的信号，则右侧就等于疑义度减去校正信道的传送速率。如果这个信道的容量小于疑义度，则右侧将大于0，且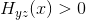
。但这是在接收信号和校正数据都已知时，所发送的不确定性。如果它大于0，则错误频率就不可能是任意小。
示例：
假定在一个二进制数位组成的序列中，随机出现错误：一个数位发生错误的概率为p，正确的概率为q=1-p。如果这些错误的位置已知，则可以进行纠正。因此，校正信道只需要发送有关这些错误位置的信息。这就相当于要传送一个信源生成的二进制数位，这些数据是1的概率为p（传送错误），是0的概率为q（传送正确）。这就一个容量为
-[p log p+q log q]
这就是原系统的疑义度。
由于上面给出的等式，传送速率R可以记为其他两种形式。有：
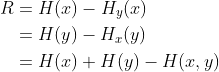
第一个定义表达式已经解读为传送的信息量减去所发送内容的不确定性。第二表达式度量的是接收内容减去由于噪声导致的部分。第三个表示式是两个数量之和减去联合熵，在某种意义上，就是两者每秒钟共有的比特数。因此，这三种表达式的意义都与直觉一致。
一个有噪声信道的容量C应当是可能实现的最大传送速率，也就是说，在信源与信道恰好匹配时的速率。因此，我们将信道容量定义为：
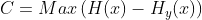
其中的最大值，是相对于所有可以用作信道输入的信源求得。如果信道是无噪声的，则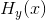
。于是，这一定义与前面已经针对无噪声信道给出的定义等价，因为信道的最大熵就是它的容量。