1. 离散无噪声信道

电传打字机和电报通讯是信息传送离散信道的两个简单例子。 一般来说，离散信道意味着可以通过一个系统，从一点向另一点传送一个选择序列，而该序列选自一个由基本符号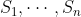组成的有限集合。假定每个符号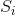的特定持续时间为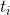秒（对于不同的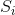，此持续时间不一定相同，比如电报中使用的点和划）。并不要求在此系统中能够传送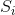的所有可能序列；可以仅允许出现特定序列。这些特定序列就是可能出现在该信道中的信号。因此，在电报中，假定这些符号为：(1) 点，先将线路闭合一个时间单位，然后再断开一个时间单位；(2) 划，线路闭合三个时间单位，然后断开一个时间单位；(3) 字符空，比如将线路断开三个时间单位；(4) 字空，线路断开六个时间单位。我们可以对允许出现的序列设定限制：不允许两个空相邻（因此，如果两个字符空相邻，则与一个字空相同）。我们现在考虑的问题是，如何度量这样一个信道的信息传输能力。

在电传打字机中，所有符号的持续时间相同，允许出现任何由32个符号组成的序列，上面的问题很容易解答。每个符号表示5比特信息。如果系统每秒传送n个符号，那自然可以说该信道的容量为5n比特/秒。这并不是说电传信道总是以这一速度传送信息——这是最大可能速率，后面将会看到，实际速率能否达到这一最大值，取决于向信道馈送信息的信源。

在更一般的情况下，符号的长度不同，而且对允许序列设有限制，我们做出如下定义：

定义：离散信道的容量C给出如下：

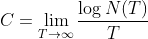
式中，N(T)是指在允许出现的信号中，持续时间为T的信号数目。

容易看出，在电传情况下，这一公式简化为前面的结果。可以证明，在人们所关注的大多数情况下，上述极限值存在且有穷。假定允许出现信号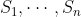的所有序列，而且这些符号的持续时间为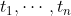。信道容量是多少呢？如果N(t)表示持续时间为t的序列数，则有：

。

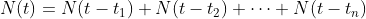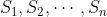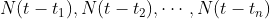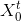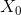该总数等于以结尾的序列数目之和，这些数目分别为。由有限差分中一个众所周知的结果可知，对于大的t值，N(t)趋近于，其中是以下特征方程的最大实数解：

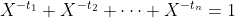
因此，

在对允许出现的序列设定了限制时，仍然能够获得这一类型的差分方程，并由该特征方程求得C。在前面提到的电报情景中，根据最后一个符号或者倒数第二个符号来计算符号序列的数目，可以得出：

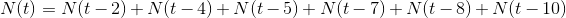
因此，C为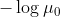，其中是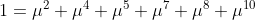的正根。求解此方程后可得C=0.539。

在对允许序列设定的限制中，有一种非常普通的类型：假设有大量可能状态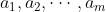，对于每种状态，只能传送集合中的特定符号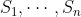（不同状态对应的子集不同）。在传输一个序列后，系统状态改为一种新的状态，具体取决于原有状态和所传送的特定符号。电报是这种情景的一个简单示例。根据最后传送的符号是不是空格，共存在两种状态。如果是空格，则接下来只能传送一个点或一个划，状态总是发生改变。如果不是空格，则可以传送任意符号，如果发送的是空格，则状态发生变化，如果不是空格，则状态保持不变。这些条件可以用如图2所示的线性图表示。交点对应于状态，连线表示一种状态下可以传送的符号及传送符号后所得到的状态。在附录1中，如果可以用这种方式来描述对允许序列设定的条件，则C存在，并可计算如下：

定理1：设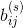是指在状态i下允许出现并导致状态j的第s个符号的持续时间，则信道容量C等于 log W，其中W为以下行列式方程的最大实根：

其中，当i = j时，，否则，等于0。

例如，在电报通讯中（图2），该行列式为：

展开后，即可得到上文针对这一情景给出的方程。

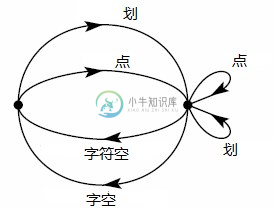
图2 用图形表示针对电报符号设置的约束条件