附录7
下面将给出一种更一般、更严格的方法,引出通信理论的核心定义。考虑一个概率度量空间,它的元素是有序对(x, y)。变量x,y被看作是可能被传送和接收的信号,它们具有较长的持续时间T。一些点的x属于一个由点x组成的子集 ,我们将所有这些点组成的集合称为
,我们将所有这些点组成的集合称为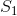 上的条带(strip),类似的,如果一些点的y都属于子集
上的条带(strip),类似的,如果一些点的y都属于子集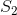 ,则将所有此类点组成的集合称为
,则将所有此类点组成的集合称为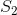 上的条带。我们将x和y划分为非重叠可测子集
上的条带。我们将x和y划分为非重叠可测子集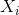 和
和 的一个集合,它们以下式近似表示传送速率R:
的一个集合,它们以下式近似表示传送速率R:
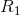
其中
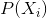 是
是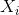 上条带的概率度量
上条带的概率度量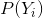 是
是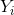 上条带的概率度量
上条带的概率度量 是这些条带交集的概率度量
是这些条带交集的概率度量
无论再如何细分,都不会使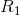 减小。将
减小。将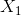 划分为
划分为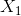 ,并令:
,并令:
因此,对于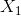 ,
,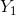 的交集,我们已经用
的交集,我们已经用
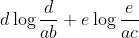 代替了
代替了
容易证明,考虑到对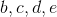 设定的限制,
设定的限制,
结果,该和值增大。因此,各种可能出现的细分构成了一个有向集合,随着细分的深入,R单调递增。我们可以明确地将 R 定义为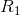 的最小上限,并将其记为:
的最小上限,并将其记为:
根据上述意义,这个积分包含了连续和离散两种情况,当然还有许多其他不能用这两种形式来表示的情景。如果 x 和 u 具有一一对应关系,从 u 到 y 的速率等于从 x 到 y 的速率,则它在这一公式中是平凡的。如果 是y的任意函数(该函数不一定可逆),则从 x 到 y 的速率大于从 x 到
是y的任意函数(该函数不一定可逆),则从 x 到 y 的速率大于从 x 到 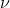 的速率,这是因为在计算近似时,y 的细分实质上是对
的速率,这是因为在计算近似时,y 的细分实质上是对 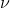 更精细再分。更一般地说,如果 y 和
更精细再分。更一般地说,如果 y 和 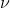 没有函数关系,而是统计相关,也就是说有一个概率测度空间(y,
没有函数关系,而是统计相关,也就是说有一个概率测度空间(y, 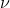 ),则
),则。这意味着对接收信号应用的任何操作,即使涉及到统计分量,也不会增大R。
还有另外一个概念,应当用一个抽象的理论公式来准确定义,那就是“维度速率”,也就是为了指定系集中的一个成员,平均每秒需要多少维度。在带限情况下,每秒种有2W个数就足够了。一般定义可构造如下。设是一个函数系集,并设
 是一个度量,用来测量在时间T上从
是一个度量,用来测量在时间T上从到
的“距离”(例如,在T时间内的RMS差)。通过选择一定数量的元素
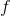 ,可以使系集中的所有元素(除去一个测度为
,可以使系集中的所有元素(除去一个测度为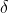 的集合之外)至少与一个所选元素
的集合之外)至少与一个所选元素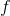 的距离不大于
的距离不大于 。设
。设是满足上述条件的最少
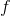 数。于是,除了一个小测度
数。于是,除了一个小测度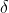 的集合之外,我们将整个空间涵盖在
的集合之外,我们将整个空间涵盖在 范围内。我们用下面的三重极限来定义该系集的维度速率
范围内。我们用下面的三重极限来定义该系集的维度速率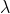 :
:
。
这是拓扑学中维度测度类型定义的推广。在一些简单的系集中,所期望的结果是明显成立的,而上式与这些简单系集的直观维度速率也是一致的。

