13. 有噪声离散信道的基本定理

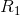要定义一个有噪声信道的容量C，这听起来似乎有些让人惊讶，因为在有噪声情况下，我们永远都无法确定地传送信息。但是，非常明确的是，如果以某种冗余方式来发送信息，那就可以减少出现错误的概率。例如，将消息重复发送许多次，并对所接收消息的不同版本进行统计研究，就可以将错误概率降到非常低。不过，有人可能希望让这一错误概率趋近于0。这绝对无法实现。如果能够实现，那就不存在一个定义严谨的容量了，只有相对于一个给定错误频率或者给定疑义度的容量；当错误标准越来越严格时，该容量就会下降。实际上，上面定义的容量C有非常明确的重要性。通过正确编码，有可能通过该信道以速率C传送信息，而错误频率或疑义度可以小到令人满意。而这一表述对于任何大于C的速率都是不成立的。如果尝试以一个高于C的速率进行传送，比如，则必然存在一个等于或大于的疑义度。而这是需要付出代价的，因为这样会具有更多的不确定性，我们实际上无法正确地获得大于C的速率。

图9中描述了这一情景。输入信道的信息速率画在横轴上，疑义度画在纵轴。阴影区域中任何高于粗线的点都可以实现，而下面的点则无法实现。这条粗线上的点通常也是无法实现的，其中两个点通常是可以实现的。

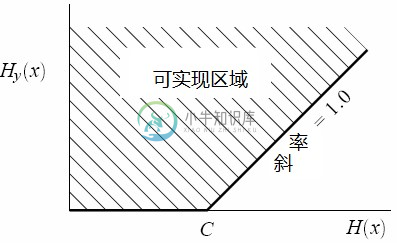
图9 信道输入的熵给定时，可能实现的疑义度

这些结果是表明C定义合理性的主要理由，现在我们将对其进行证明。

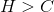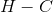定理11：设一个离散信道的容量为C，一个离散信源的熵（每秒）为H。如果，则存在一个编码系统，可以通过该信道传送该信源的输出内容，而错误频率达到任意小（或者说，疑义度任意小）。如果，则有可能对信源进行编码，使得疑义度小于，其中为任意小。不存在能够使疑义度小于的编码方法。

为了证明这一定义的第一部分，并不是给出一个具有期望性质的编码方法，而是证明在特定的代码组中，必然存在这样一种编码。事实上，我们会将错误频率在这个组中求平均，从而证明这个平均值可以小于。如果一个数组的平均值小于，则这个集合中必然存在至少一个数字小于。这样就可以确定所需要的结果。

有噪声信道的容量C已经定义如下：

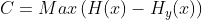
其中，x为输入，y为输出。此最大值是针对所有可以用作信道输入的信源求取的。

设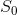是实现最大容量C的信源。如果任何信源都不能实际达到这个最大值，则设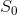是最接近能够给出最大速率的信源。假定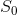用作该信道的输入。我们考虑一个长持续时间T的传送与接收序列。以下表述是成立的：

1. 传送信号分为两组，一个高概率组，大约有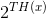个成员，其余序列的总概率非常小。

2. 类似的，接收信号也有一个大约有个成员的高概率集合，其余序列组成一个小概率集合。

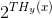3. 每个高概率输出可以由大约个输入生成。所有其他情景的的总概率很小。

这些表述中的“小”和“大约”等用词可以用和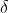来表示，如果允许T增大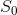，趋近于可实现最大值的信源，则所有和都趋近于0。

这一情景总结于图10中，其中，输入序列为左侧的点，输出序列为右侧的点。交叉线组成的扇形表示可能一个典型输出的原因范围。

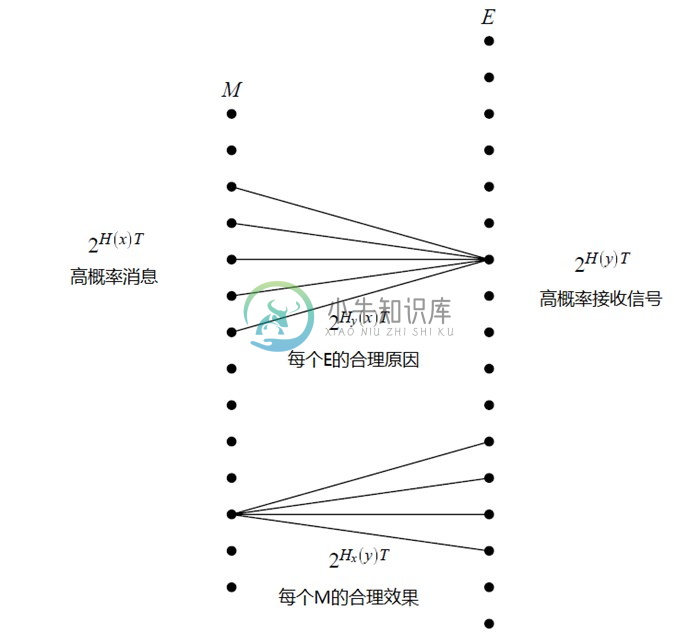
图10 信号输入与输出关系的示意表示

现在假定我们有另外一个以速率R生成信息的信源，其中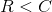。在周期T中，这一信源有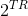条高概率消息。我们希望以某种方式将这些消息与可以作为信道输入的一组选择关联起来，以实现小的错误频率。我们将以所有可能方式来设定这一关联（但是，仅使用由信源确定的高概率输入组），并针对这一大类可能存在的编码系统求平均错误频率。这相当于将这些消息与持续时间为T的信道输入随机关联起来时，计算误差频率。假定观察到一个特定的输出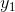。在可能导致的原因集中，超过一条消息的概率为多少呢？在个点中随机分布着条消息。因此，一个特定点被选作消息的概率为：

。

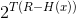扇形中所有点都不是消息（真正的原始消息除外）的概率为：

。

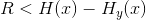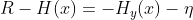现在，，所以，其中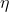为正数。相应地，当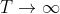时：

趋近于

。

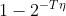因此，错误概率趋近于0，定理的第一部分得证。

注意到，我们只能以C比特/秒的速率发送来自信源的内容，完全忽略所生成的其余信息，由此容易证明该定理的第二部分。在接收器处，被忽略部分给出的疑义度为，所传送部分只需要增加。采用许多其他方法都可以达到这一极限，在考虑连续情景时将会看到这一点。

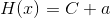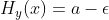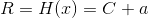该定理的最后一种表述可以由C的定义直接推出。假定我们可以采用某种方式对信源以进行编码，以获得疑义度，其中为正数。因此，有，且：

其中为正数。而根据C的定义，它是 的最大值，矛盾。

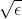实际上，我们所证明的内容并不仅限于定理中的所述内容。如果一个数字集合的平均值在其最大值的范围内，则这些数字中，最多有部分与最大值之差大于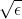。由于是任意小，所以我们可以说几乎所有这些系统都任意接近于理想编码。