7. 信源的熵
考虑上面讨论的具有有限种状态的离散信源。对于每种可能存在的状态i,都存在一组表示生成各种可能状态j的概率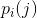 。因此,对于每种状态都存在一个熵
。因此,对于每种状态都存在一个熵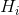 。信源的熵定义为这些
。信源的熵定义为这些 的加权平均,加权值为所考虑状态的发生概率:
的加权平均,加权值为所考虑状态的发生概率:
这是信源关于每个文本符号的熵。如果马尔可夫过程以某一确定时间速率执行,则还存在一个关于每秒的熵:
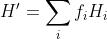
其中 是状态i的平均频率(每秒钟的发生次数)。显然:
是状态i的平均频率(每秒钟的发生次数)。显然:
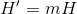
其中m是平均每秒钟生成的符号数。H或H'度量该信源每个符号或每秒钟生成的信息数。如果对数底数为2,H和H'表示每个符号或每秒的比特数。
如果连续符号相互独立,则H就是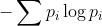 ,其中的
,其中的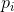 是符号i的概率。假定我们在此情况下考虑一个包含N个符号的长消息。它将以很高的概率包含
是符号i的概率。假定我们在此情况下考虑一个包含N个符号的长消息。它将以很高的概率包含 个第1符号,
个第1符号,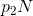 个第2符号,以此类推。因此,这一特定消息的概率大约为:
个第2符号,以此类推。因此,这一特定消息的概率大约为:
或者,
于是,H近似等于对于个一个典型长序列的概率的倒数求对数,再除以该序列中的符号数。同一结果对于任意信源都是成立的。我们可以更准确地表述为(见附录3):
定理3:给定任意ε>0和δ>0,我们可以求得一个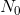 ,使得任意长度
,使得任意长度的序列都属于以下两个类别之一:
一个总概率小于ε的集合。
不属于上述集合的所有序列,这些序列的概率都满足不等式:
换言之,当N很大时,我们几乎可以肯定会非常接近于H。
一个密切相关的结果讨论了不同概率的序列数目。再次考虑长度为N的序列,并按频率的降序排列它们。假定我们要按照序列的概率大小,从这个序列集中取出一些序列(先取概率最大者)。对于一个给定的概率值q,我们将n(q)定义为使所取序列概率总和达到q而必须从集合中取出的序列数目。
定理4:
其中,q不等于0和1。
当我们仅考虑总概率为q、最可能出现的序列时,我们可以将log n(q)解读为指定该序列所需要的比特数。因此,就是在这种指定方式中,每个符号的比特数。该定理说明,这一数值与q无关,等于H。对于具有合理可能性的序列,无论我们如何解读“具有合理可能性”,此种序列个数的对数增长率都是H。根据这些结果(在附录3中进行证明),在大多数情况下,我们都可以认为这些长序列仅有
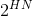 个,每个序列的概率为
个,每个序列的概率为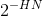 。
。
下面的两个定理表明,H和H'可以通过求极限运算,直接由消息序列的统计量得出,不需要涉及状态,也不需要状态之间的转换概率。
定理5: 设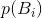 是信源中发出的一个符号序列
是信源中发出的一个符号序列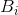 的概率。令
的概率。令

其中,该求和运算是针对所有包含N个符号的序列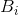 执行。因此,
执行。因此,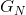 是N的单调减函数,且:
是N的单调减函数,且:
。
定理6:设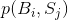 是序列
是序列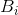 之后跟有符号
之后跟有符号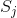 的概率,
的概率,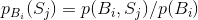 是出现
是出现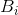 之后出现
之后出现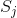 的条件概率。令:
的条件概率。令:

其中,该求和运算是针对所有包括N-1个符号的块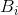 及针对所有符号
及针对所有符号 执行的。则
执行的。则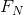 是N的单调减函数,
是N的单调减函数,
及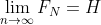 。
。
这些结果在附录3中进行推导。它们表明,只需要考虑遍布1,2,...,N个符号的序列的统计结构,就可以获得对H的级数近似。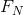 是更佳近似。事实上,
是更佳近似。事实上,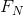 是上述信源类型的N阶近似。如果统计影响不会扩展到N个以上的符号,也就是说,如果在知道前(N-1)个符号之后,出现下一个符号的条件概率不会因为知道了更早之前的符号而发生变化,则
是上述信源类型的N阶近似。如果统计影响不会扩展到N个以上的符号,也就是说,如果在知道前(N-1)个符号之后,出现下一个符号的条件概率不会因为知道了更早之前的符号而发生变化,则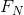 。
。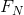 当然是在已知前(N-1)个符号时,下一个符号的条件熵,而
当然是在已知前(N-1)个符号时,下一个符号的条件熵,而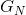 则是包含N个符号的块中每个符号的熵。
则是包含N个符号的块中每个符号的熵。
一个信源的熵除以它在使用相同符号时所能达到的最大熵,所得的比值称为相对熵。这是我们利用相同字符表进行编码时,可能达到的最大压缩比。1减去相对熵的差值称为冗余度。如果不考虑超过大约八个字符以上的统计结构,普通英语的冗余度大约为50%。也就是说,在我们用英文写作时,所写内容中有一半由英语的结构决定,另一半是自由选择的。由几种相互独立的方法都可以求得数字50%,这些方法给出的结果都在这一数字附近。一种方法是计算英文近似表达的熵。第二种方法是从一段英文文本样本中删除一定比例的字符,然后让别人尝试恢复原文。如果在删除50%的字符后,还能恢复出原文,则冗余度一定大于50%。第三种方法依赖于密码学中的一些已知结果。
“基础英语”和James Joyce的“Finnegans Wake”一书代表着英文散文中冗余度的两个极端。基础英文的词汇不超过850个单词,冗余度非常高。在将一段文字翻译为基础英文时,其篇幅会扩展许多,这一现象反映了基础英语的高冗余度。而另一方面,Joyce扩充了词汇,据说是为了实现语义内容的压缩。
一种语言的冗余度与纵横填字字谜的存在有关。如果冗余度为0,则任何字符序列都是该语言中的合理文本,任何两维字符阵列都可以构成一个纵横字谜。如果冗余度太高,为使大型纵横字谜成为可能,该语言要设置太多的约束条件。一种更为详尽的分析表明,如果我们假定该语言设定的约束条件在实质上是相当混乱和随机的,那在冗余度为50%时,大型纵横字谜游戏刚好成为可能。如果冗余度为33%,则三维交叉字谜应当有可能实现,以此类推。

