22. 线性滤波器中的熵损失

定理14：一个系集的带宽为W，其熵为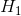（每自由度），如果使该系集通过一个特性函数为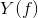的滤波器，则输出系集的熵为：

。

此滤波器的运算实际上就是坐标系的线性变换。如果将不同的频率分量看作原坐标系，则新的频率分量实际上就是原频率分量乘以相应的因子。坐标变换矩阵的对角线元素实际上就是这些坐标。该变换的雅可比行列式为（对于n个正弦分量和n个余弦分量）：

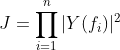
其中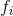在带宽W内等间隔分布。因此，上式变为极限值：

。

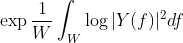由于J是常数，所以它的均值是相同量，另外，根据在坐标变换时熵的变化定理，可以得出结果。我们还可以用熵功率来表达。因此，如果第一个系集的熵功率为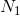，则第二个系集的熵功率为：

。

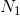最终的熵功率等于原熵功率乘以滤波器的几何平均增益。如果该增益的单位为db，则输出熵功率的增大值将等于频宽W上的算术平均db增益。

在表1中，对于几种理想增益特性曲线计算了熵功率损失（也以db为单位）。这些滤波器的冲激响应也以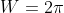给出，假定相位为0。

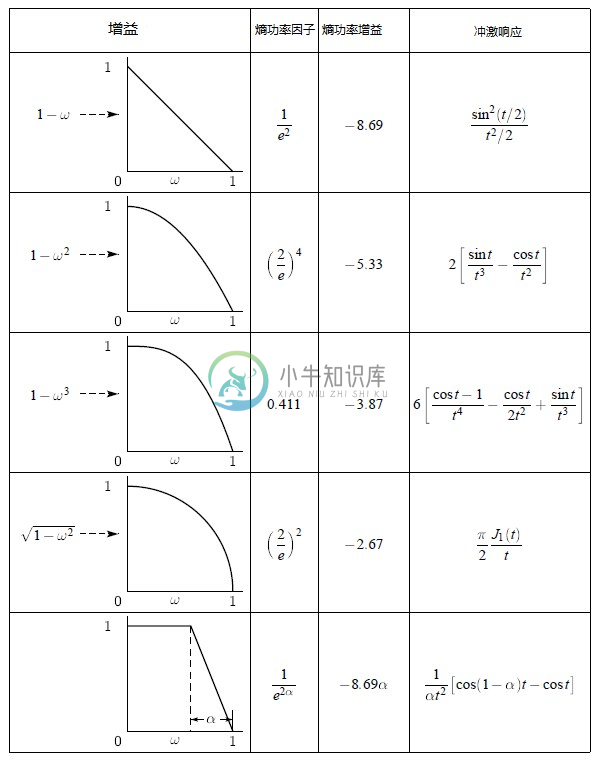
表1

其他许多情况下的熵损失都可以由这些结果计算得出。例如，第一种情况中的熵功率因子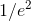也适用于通过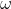轴的保测变换，由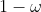得到的任意其他增益特性。具体来说，线性增益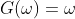或介于0与1之间的“锯齿”特性都具有同样的熵损失。增益取倒数时，其因子也取倒数。因此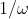，的因子为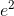。将任意功率增大该增益，都会使该功率乘以这一因子。