28. 信源在给定保真度评价函数下的信息生成速率

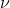我们现在要确定一个连续信源生成信息的速率了。已知信源的和由距离函数确定的评价，假定该距离函数在x和y上都是连续的。对于一个具体的系统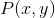，其质量可以衡量如下：

此外，与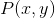对应的二进制数位流的速率为：

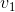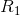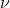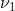对于给定的消息复现质量，信息生成速率的定义为：使固定为，改变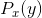时得到的最小R值。即：

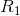
其服从以下约束条件：

这意味着，我们实际上考虑了所有可以使用、以所需保真度进行传送的通信系统。对于每一个系统计算传送速率（单位为比特/秒），并选择速率最低的那个系统。 这个最低速率就是在所讨论保真度下为信源指定的速率。

由以下结果可以看出这一定义的合理性：

定理21：如果对于一个评价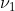，一个信源的信息生成速率为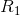，一个信道的容量为C，只要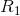，就有可能对信源的输出进行编码，通过该信道，以任意接近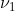的保真度进行传送。如果，则不可能实现。

通过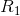的定义和前面给出的结果，马上可以得出定理的第二部分。如果该表述错误，那就可以通过一个容量为C的信道以超过C比特/秒的速率传送了。定理的第一部分可以通过一种用于证明定理11的类似方法来证明。首先，我们将(x,y)空间分为大量的小单元格，并像离散情景中一样进行表示。当单元格非常小时，由于假定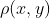是连续的，所以这一过程使评价函数的变化不会超过一个任意小的量。假定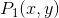是一个具体系统，它使该速率取最小值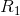。我们从高概率的y中随机选择一个集合，其中包含

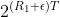
个成员，式中，当时，。当T很大时，每个选定点都会通过一条出现概率很高的直线（如图10中所示）连接到x的一个集合。采用定理11证明过程中的类似计算过程，可以证明：当T很大时，对于y的几乎所有可能选择，几乎所有x都会被一个以所选y点为起点的扇形所覆盖。通信系统的操作如下：为选定点指定二进制数。如果发送一条消息x，当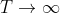时，x位于至少一个扇形中的概率趋近于1。以适当的编码方式，通过该信道传送对应的二进制数，实现很低的错误概率（如果存在几个对应的二进制数，则传送其中任意选定的一个）。由于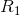，所以这是可能实现的。在接收端，重构出相应的y，并当作恢复出来的消息。

只要使T足够大，就可以使这一系统的评价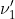任意接近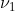。其原因是：对于每个长的消息样本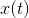和恢复出来的消息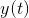，该评价（以概率1）接近于。

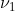值得注意的是，在这个系统中，接收消息中的噪声实际上是传送器中的一般性量化过程产生的，而不是由信道中的噪声产生的。它多少类似于PCM中的量化噪声。