19. 带限函数系集

如果一个时间函数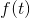的带宽局限于0至W个周期/秒，只需要给出该函数在一系列间距为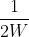秒的离散点上的分量，就可以利用以下方式确定该函数。

定理13：设中没有超过W的频率，则：

，

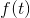其中：

。

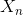在这个展开式中，表示为正交函数之和。各项的系数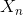可以看作是一个无限维“函数空间”中的坐标。在这个空间中，每个函数准确地对应一个点，每个点对应一个函数。

如果0到时刻T之外的所有坐标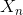都是0，则可以认为一个函数基本上局限于时刻T。在这种情况下，除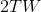之外的所有坐标都是0。因此，带宽限制于W、持续时间为T的函数对应于一个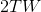维空间中的点。

带限为W、持续时间为T的函数子集对应于这个空间中的一个区域。例如，总能量小于或等于E的函数对应于一个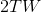维球面内的点，其半径为。

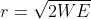一个持续时间和带宽有限的函数系集可以用相应n维空间中的一个概率分布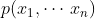来表示。如果该系集不受时间限制，是可以用一个给定区间T中的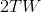个坐标来大体表示该区间T中的函数部分，用概率分布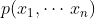给出该系集在该持续时间区间内的统计结构。