18. 函数的集合与系集
在连续情景中,我们不得不处理函数的集合和函数的系集。由函数集的名字可以看出,它就是一组函数,通常是一个变量——时间的函数。为描述函数集,我们可以给出集合中各种函数的显式表达式,也可以给出只有集合中的函数才拥有的性质。下面是一些示例:
由以下函数组成的集合:
 。
。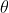 的每个具体值确定了集合中的一个特定函数。
的每个具体值确定了集合中的一个特定函数。一个由时间函数组成的集合,其中包含频率不超过W周期/秒的所有时间函数。
一个由带宽局限于W、幅度不超过A的所有函数组成的集合。
将所有英文语音信号表示为时间函数组成的集合。
函数的系集(ensemble)是一个函数集合再加上一个概率度量,利用这一度量,我们可以确定集合中一个具有特定性质的函数的概率。例如,对于以下集合:
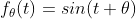 ,
,
我们可以给出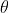 的一个概率分布,
的一个概率分布,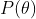 。该集合就变成一个系集。
。该集合就变成一个系集。
函数系集的另外一些例子包括:
一个有限函数集
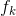 ,其中
,其中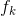 的概率为
的概率为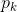 。
。一个有限维的函数簇:
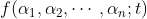
加上参数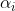 的一个概率分布:
的一个概率分布: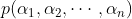 。
。
例如,我们可以考虑以下式定义的系集
其中的幅度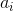 独立、正态分布,相位
独立、正态分布,相位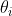 在0到
在0到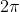 之间均匀独立分布。
之间均匀独立分布。系集
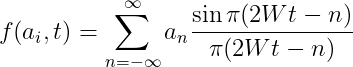
其中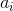 为正态独立分布,都具有相同的标准差
为正态独立分布,都具有相同的标准差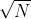 。这是一种“白”噪声的表示,其频带限于0到W周期/秒,平均功率为N。
。这是一种“白”噪声的表示,其频带限于0到W周期/秒,平均功率为N。设分布在t轴上的各个点服从泊松分布。在每个选定点上放置一个函数
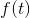 ,并添加不同的函数,给出系集:
,并添加不同的函数,给出系集:
其中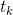 是服从泊松分布的点。这一系集可以看作是一种脉冲或散粒类型的噪声,其中所有脉冲都相同。
是服从泊松分布的点。这一系集可以看作是一种脉冲或散粒类型的噪声,其中所有脉冲都相同。英文语音函数的集合,其概率度量由普通应用中的发生频率给出。
一个函数系集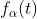 ,如果将所有函数都平移任意固定时间量后,会得到同一系集,则说这个系集是平稳的。如果
,如果将所有函数都平移任意固定时间量后,会得到同一系集,则说这个系集是平稳的。如果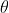 在0和
在0和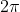 之间均匀分布,则系集:
之间均匀分布,则系集:
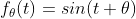
是平稳的。如果我们将每个函数平移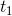 ,则可以得到:
,则可以得到:
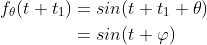
其中 在0和
在0和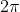 之间均匀分布。每个函数都发生了变化,但系集作为整体在转换后是不变的。上面给出的其他示例也是平稳的。
之间均匀分布。每个函数都发生了变化,但系集作为整体在转换后是不变的。上面给出的其他示例也是平稳的。
如果一个系集是平稳的,而且集合中任何一个概率不是0和1的函数子集都不是平稳的,则说这个系集是各态历经的。系集:
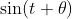
是各态历经的。这些函数的任何一个概率不为0和1的子集,经过任何时间平移后,都不会转换为它自己。另一方面,如果a为均匀分布, 为均匀分布,则系集
为均匀分布,则系集
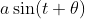
是平稳的,但不是各态历经的。例如,a介于0与1之间的函数子集是平移的。
在给出的示例中,3和4是各态历经的,5也可以看作是各态历练的。如果一个系集是各态历经的,我们可以大致地说,这个集合中的每个函数都是该系列的一个代表。更准确地说,我们知道对于一个各态历经系集,系集上任意统计值的平均值(以概率1)等于对集合内一个具体函数各时间平移版本求得的平均值。大致来说,随着时间的推移,可以预期每个函数都会以适当的频率遍历集合中任意函数的所有状态。
我们对大量函数执行各种操作可以获得新的函数,同样,对系集进行操作也可以获得新的系集。例如,假定有一个函数系集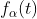 和运算符T,它对每个函数
和运算符T,它对每个函数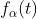 进行运算后,得到函数
进行运算后,得到函数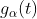 :
:
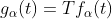 。
。
利用集合 的概率度量,为集合
的概率度量,为集合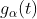 定义概率度量。
定义概率度量。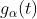 函数的一个特定子集的概率等于某个
函数的一个特定子集的概率等于某个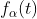 函数子集的概率,这些
函数子集的概率,这些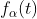 函数经过运算T后,生成给定g函数子集的成员。从物理上来说,这相当于将该系集通过某一设备,比如一个滤波器、整流器或调制器。该设备的输出函数构成系集
函数经过运算T后,生成给定g函数子集的成员。从物理上来说,这相当于将该系集通过某一设备,比如一个滤波器、整流器或调制器。该设备的输出函数构成系集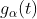 。
。
如果一个设备或运算符T对输入移位后,只是让输出也同样移位,则称之为“时不变的”,也就是说,如果对于所有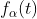 和所有
和所有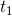 ,可以由
,可以由

可以推出:
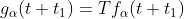
则说它是时不变的。容易看出(见附录5),如果T是时不变的,而且输入系集是平稳的,则输出系集也是平稳的。同样,如果输入是各态历经的,则输出也是各态历经的。
滤波器或整流器在所有时间平稳情况下,都是时不变的。而调制操作则不是,因为载波相位呈现一定的时间结构。但是,如果平移量是该载波周期的倍数,则调制操作也是时不变的。
维纳已经指出了物理设备在时间平稳情况下的不变性与傅里叶理论之间的密切关系。他已经证明:如果一个设备是线性时不变的,则傅里叶分析是处理该问题的合适数学工具。
由连续信源(例如语音)生成的消息、发送器生成的信号,以及干扰噪声,都可以很准确地用函数系集进行数学表示。维纳已经强调过,通信理论应当关心的不是对特定函数的操作,而是对函数系集的操作。通信系统不是为特定的语音函数设计的,更不是为正弦函数设计的,而是为语音函数的系集设计的。

