8. 编解码处理的表示

我们还必须用数学方式来表示发送器和接收器在对信息进行编解码时所执行的处理。发送器和接收器都将被称为转换器(transducer)。转换器接收一个符号序列（称为输入符号序列），输出另外一个符号序列（称为输出符号序列）。转换器可能具有内部存储器，使其输出不仅依赖于当前的输入符号，还依赖于过去的历史输入。我们假定内部存储器是有限的，也就是说转换器存在m种可能状态（m为一个有限数），且其输出是当前状态和当前输入符号的函数。下一个状态将是这两个量的另一个函数。因此，转换器可以用两个函数来描述：

其中：

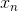是第n个输入符号，
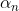是在送入第n个输入符号时，转换器的状态，
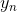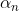是在状态为时送入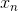时生成的输出符号（或者输出符号序列）。

如果一个转换器的输出符号与一个第二转换器的输入符号相同，可以将这两个转换器串联在一起，所得到的装置还是一个转换器。如果存在一个第二转换器，它对第一个转换器的输出进行处理，并恢复出原来的输入内容，则说第一个转换器是非奇异的，将第二个转换器称为它的逆。

定理7：一个有限状态转换器在由有限状态的统计信源驱动时，其输出是一个有限状态统计信源，其熵（每单位时间）小于或等于输入的熵。如果转换器是非奇异的，则两者相等。

令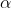表示信源的状态，该信源生成一个符号序列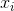；令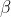表示转换器的状态，该转换器在其输出中生成符号块。这个组合系统可以用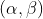对的“积状态空间”表示。如果可以生成一个x，将变为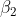，则可以用一条线将该空间中的两个点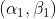和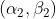连在一起，并在线上给出在此情况下出现x的概率。在线上标出由转换器生成的符号块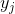。可以针对各个状态求加权和来计算输出的熵。如果首先针对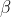求和，则所得到的每个项都小于或等于针对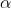求出的相应项，因此，这个熵不会增大。如果转换器是非奇异的，则将其输出连接到逆转换器。如果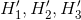分别是信源、第一转换器和第二转换器的输出熵，则，因此可得。

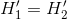假定我们对于可以出现的序列类型设定了一套约束条件，可以用图2中的线图加以表示。如果向各个将状态i连至状态j的线上指定概率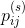，它将会变成一个信源。存在一种特定的指定方式，使所得到的熵取最大值（见附录4）。

定理8：将一套约束条件看作一个信道，设其容量为。如果我们指定：

其中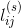，是由状态i导致状态j的第s个符号的持续时间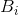，满足：

则，H为最大值，并等于C。

通过正确地指定转换概率，一个信道上的符号的熵可以达到最大值，也就是信道容量。