4. 马尔可夫过程的图形表示

上文所述类型的随机过程在数学上称为离散马尔可夫过程，在参考文献中有详尽研究。一般情况可以描述如下：一个系统存在有限种可能“状态”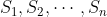。此外，还有一组转换概率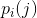，也就是当系统为状态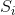，接下来进入状态的概率。为使此马尔可夫过程表示信源，只需要假定每次从一种状态转换到另一状态时，生成一个字符即可。这种状态对应于先前字符产生的“影响残余”。

此情景可以用图3，4，5表示。“状态”为图中的交点，转换概率和所生成的字符在相应线的旁边给出。图3表示第2节的例B，图4对应于例C。在图3中，由于连续字符相互独立，所以只存在一种状态。在图4中，所存在的状态数与字符相同。如果构造一个三连字示例，则最多存在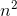种状态，对当前选定字符之前的可能字符对相对应。图5是例D中单词结构的对应图。这里的S表示“空(space)"符号。

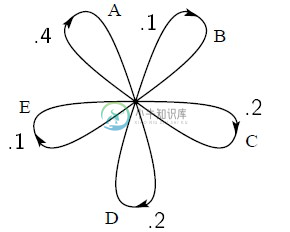
图3 例B中信源的对应图

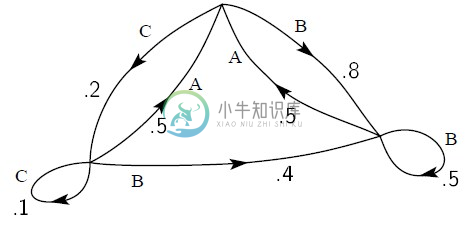
图4 例C中信源的对应图

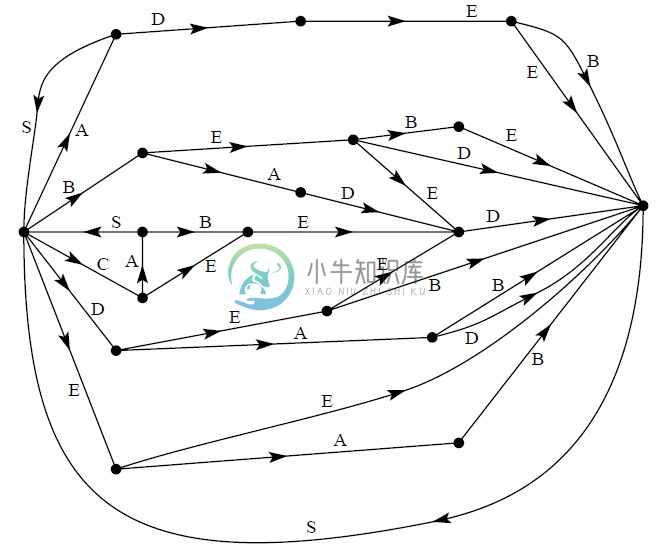
图5 例D中信源的对应图