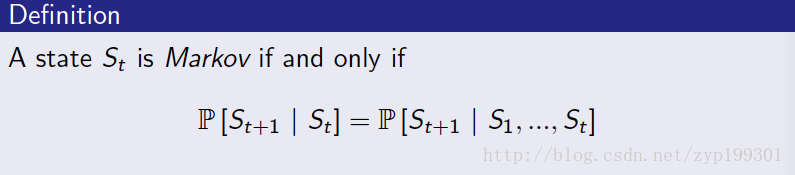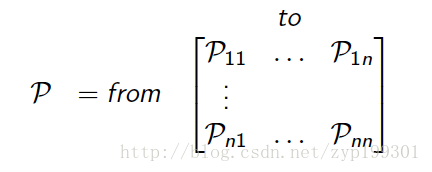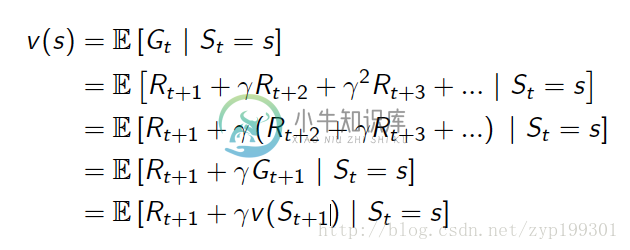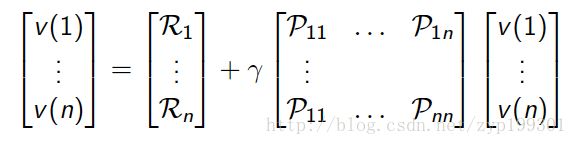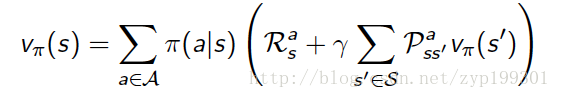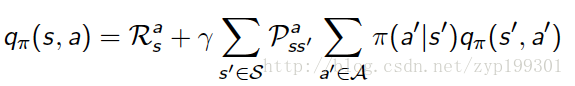马尔可夫决策过程MDP
马尔可夫决策过程正式的描述了增强学习所处的环境,在这个环境中,所有都是可观测的。所有的增强学习都可以被转化为MDP。
- 连续MDP的最优控制过程(Optimal control)
- Partially observable problems也可以转化为MDP
- 多臂赌博机问题
马尔可夫特性
意味着未来的状态只与现在所处的状态有关。过去的history都可以丢弃。
状态转移矩阵
这里矩阵代表状态转移时候的矩阵,每一行sum为1。
马尔可夫过程(Markov Process)
马尔可夫过程是一个二元组,是一个无记忆的随机过程,是一连串的状态序列具有马尔可夫特性。给出Definition.
S是状态的集合,P是转移矩阵。
马尔可夫奖励过程(Markov Reward Process)
MRP是带有价值的马尔科夫链,相对于马尔可夫过程,添加了Reward函数,和折现因子γ。给出MRP的定义。

奖励函数在于基于当前时间t的状态下,下一刻获得奖励。它是状态绑定的。
回报(return)
回报是从时间t开始(不包括时间t),到结束状态的总体的折现回报。距离当前的时间越远,折现因子的阶数越大。这里代表着对于未来的不确定性。
折现因子为0时代表着这在意当前reward
折现因子为1代表对于未来的远视,计算全额的回报
这里有一个问题,为什么对于未来回报做了折现?
- 没有对于未来的完美模型,无法对于未来的不确定性建模(感觉如果诞生了量子计算机,能过模拟从宇宙大爆炸全过程,就可以对既定现实建模了)
- 数学上方面计算,给予折现
- 避免循环中无限的回报(当未来一直在循环时,回报在循环中无限了,没法计算,我的理解,如果未来某个状态一直循环,那么其可以继续延伸很多个状态,也同样没法计算啊,不太了解,标注)
- 更在意即时回报,(视频讲的涉及动物特性,blabla,觉得还是有些诡辩)
value function 价值函数V(s)
MRP过程相对于MP是增加价值的,那么价值函数就很重要。价值函数代表着在状态S下,对于长期价值的期望。
Bellman Equation for MRPs贝尔曼等式
价值函数被拆分为两个方面,一个是即时的回报Rt+1,一个是对于未来所有状态的折现回报。
那么根据贝尔曼等式,价值函数的公式就被演化为。
这样,回报就变为
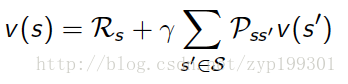
这里的Rs是出了当前状态就要加的回报,接着加上下一个状态的函数乘上转移矩阵。既然有向量形式,就有矩阵形式。
贝尔曼等式我们可以看出来是一个线性的等式,这样一个等式,可以直接计算,左右移,然后求逆。但是计算是一个复杂度的O(n3)过程。所有直接计算只能用于小型的MRP。有许多迭代算法用于大型MRP计算,
- 动态编程
- 蒙特卡洛 提升
- 时差学习
MDP
终于讲到MDP!
相比MRP,MDP又加入了动作的有限集合。A Markov decision process (MDP) is a Markov reward process with decisions.这句话很好理解。Decison (actions)是决策过程的精髓。所以,奖励函数和转移矩阵都要在动作的条件之上。
policy
这里的policy完全定义了agent的行为,MDP的policy只依赖于当前的状态,同时,他是静态的。
给予一个五元组MDP和一个policyπ。整个序列就要加入policy概率。
Value Function
value function 有两个,一个是state-value,一个是action-value。第一个state-value还是之前的但是意味着在当前的状态下,执行policy的期望回报。
第二个以为这,在当前的状态的下,采取actions,这里很关键,following policy的回报。action是很关键的。
这时,贝尔曼等式同样适用两个value function。
最优价值函数-Optimal Value Function
最优价值函数能够直接解决MDP问题,即我们能找到问题最后的最大Reward.
我们可以看出来最优价值函数就是找出最大的价值函数。同理,我们也要寻找最优的policy,对于任意一个MDP过程,都存在一个最优政策比其他政策好。所有的最优政策都要获得一样的价值函数,(因为最优的路可能有很多条,但是他们的价值最优只有一个),如何去找最优的政策,在于找到q星。如果他是action-value最优,就去选择做这个动作。
同样的,对于最优价值函数,Q和V。我们也可以用贝尔曼方程,推导是一样的。但是过程中,我们要取的最大化。
Solving the Bellman Optimality Equation
贝尔曼最优等式是非线性的,因为是求最大。同时,没有显式求解方法。这就要迭代取求解。
- Value Iteration
- Policy Iteration
- Q-learning
- Sarsa
整个过程MDP都在于给出基本概念,为了以后找出最优的action,找出最优的policy,在于最大化Reward的过程。在这里有两个问题,一个是如何保证马尔可夫模型的完善性,这在于我们假定现在所处的状态是随机的。第二,如何确定对于未知风险的考量,这个我们需要把无风险的MDP转化为风险MDP,或者直接在Reward中加入对风险的折扣。