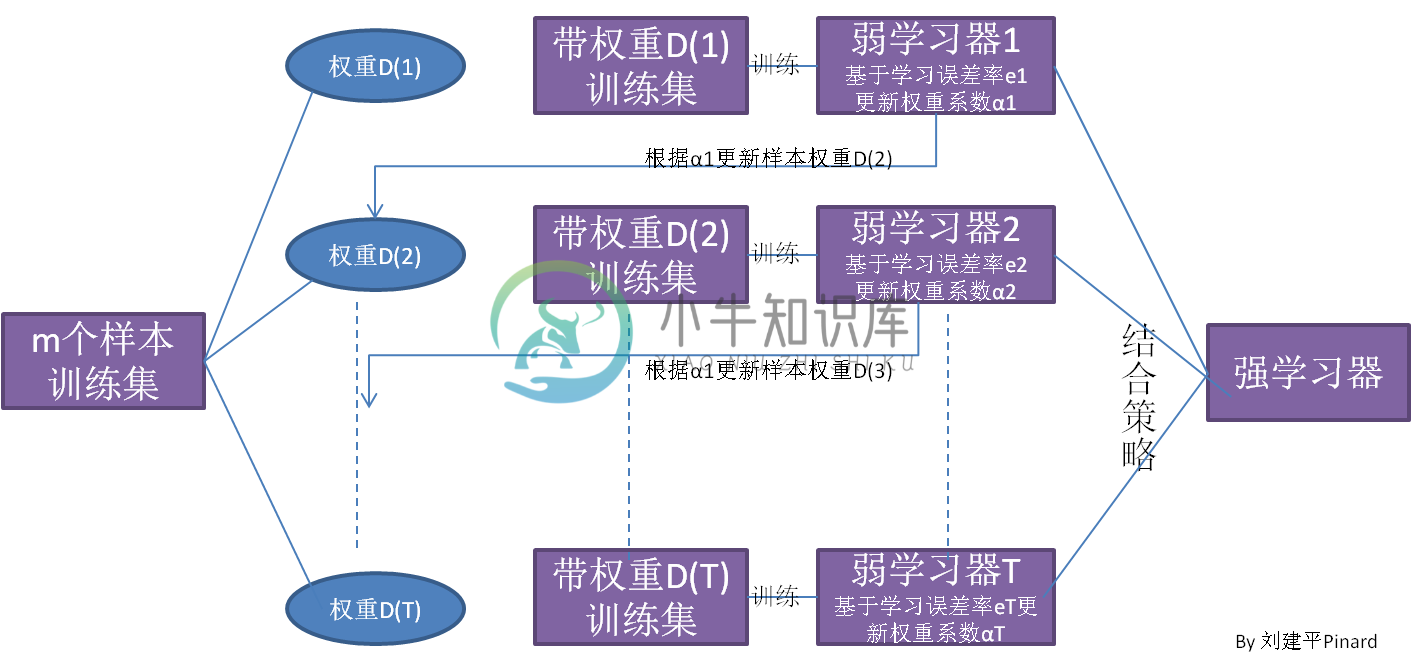
在集成学习原理中，我们已经讲到了boosting算法系列的基本思想，如下图：

从图中可以看出，Boosting算法的工作机制是首先从训练集用初始权重训练出一个弱学习器1，根据弱学习的学习误差率表现来更新训练样本的权重，使得之前弱学习器1学习误差率高的训练样本点的权重变高，使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2.，如此重复进行，直到弱学习器数达到事先指定的数目T，最终将这T个弱学习器通过集合策略进行整合，得到最终的强学习器。

不过有几个具体的问题Boosting算法没有详细说明。

1）如何计算学习误差率e?

2) 如何得到弱学习器权重系数$$alpha$$?

3）如何更新样本权重D?

4) 使用何种结合策略？

只要是boosting大家族的算法，都要解决这4个问题。那么Adaboost是怎么解决的呢？

2. Adaboost算法的基本思路

我们这里讲解Adaboost是如何解决上一节这4个问题的。

假设我们的训练集样本是$$T={(x_1,y_1),(x_2,y_2), ...(x_m,y_m)}$$

训练集的在第k个弱学习器的输出权重为$$D(k) = (w_{k1}, w_{k2}, ...w_{km}) ;;; w_{1i}=frac{1}{m};;; i =1,2...m$$

首先我们看看Adaboost的分类问题。

分类问题的误差率很好理解和计算。由于多元分类是二元分类的推广，这里假设我们是二元分类问题，输出为{-1，1}，则第k个弱分类器$$G_k(x)$$在训练集上的加权误差率为$$e_k = P(G_k(x_i) neq y_i) = sumlimits_{i=1}^{m}w_{ki}I(G_k(x_i) neq y_i)$$

接着我们看弱学习器权重系数,对于二元分类问题，第k个弱分类器$$G_k(x)$$的权重系数为$$alpha_k = frac{1}{2}logfrac{1-e_k}{e_k}$$

为什么这样计算弱学习器权重系数？从上式可以看出，如果分类误差率$$e_k$$越大，则对应的弱分类器权重系数$$alpha_k$$越小。也就是说，误差率小的弱分类器权重系数越大。具体为什么采用这个权重系数公式，我们在讲Adaboost的损失函数优化时再讲。

第三个问题，更新样本权重D。假设第k个弱分类器的样本集权重系数为$$D(k) = (w_{k1}, w_{k2}, ...w_{km})$$，则对应的第k+1个弱分类器的样本集权重系数为$$w_{k+1,i} = frac{w_{ki}}{Z_K}exp(-alpha_ky_iG_k(x_i))$$

这里$$Z_k$$是规范化因子$$Z_k = sumlimits_{i=1}^{m}w_{ki}exp(-alpha_ky_iG_k(x_i))$$

从$$w_{k+1,i}$$计算公式可以看出，如果第i个样本分类错误，则$$y_iG_k(x_i) < 0$$，导致样本的权重在第k+1个弱分类器中增大，如果分类正确，则权重在第k+1个弱分类器中减少.具体为什么采用样本权重更新公式，我们在讲Adaboost的损失函数优化时再讲。

最后一个问题是集合策略。Adaboost分类采用的是加权平均法，最终的强分类器为$$f(x) = sign(sumlimits_{k=1}^{K}alpha_kG_k(x))$$

接着我们看看Adaboost的回归问题。由于Adaboost的回归问题有很多变种，这里我们以Adaboost R2算法为准。

我们先看看回归问题的误差率的问题，对于第k个弱学习器，计算他在训练集上的最大误差$$E_k= max|y_i - G_k(x_i)|;i=1,2...m$$

然后计算每个样本的相对误差$$e_{ki}= frac{|y_i - G_k(x_i)|}{E_k}$$

这里是误差损失为线性时的情况，如果我们用平方误差，则$$e_{ki}= frac{(y_i - G_k(x_i))2}{E_k2},$$如果我们用的是指数误差，则$$e_{ki}= 1 - exp(frac{-y_i + G_k(x_i))}{E_k})$$

最终得到第k个弱学习器的 误差率$$e_k = sumlimits_{i=1}^{m}w_{ki}e_{ki}$$

我们再来看看如何得到弱学习器权重系数$$alpha$$。这里有：$$alpha_k =frac{e_k}{1-e_k}$$

对于更新样本权重D，第k+1个弱学习器的样本集权重系数为$$w_{k+1,i} = frac{w_{ki}}{Z_k}alpha_k^{1-e_{ki}}$$

这里$$Z_k$$是规范化因子$$Z_k = sumlimits_{i=1}{m}w_{ki}alpha_k{1-e_{ki}}$$

最后是结合策略，和分类问题一样，采用的也是加权平均法，最终的强回归器为$$f(x) = sumlimits_{k=1}^{K}(lnfrac{1}{alpha_k})G_k(x)$$

3. AdaBoost分类问题的损失函数优化

刚才上一节我们讲到了分类Adaboost的弱学习器权重系数公式和样本权重更新公式。但是没有解释选择这个公式的原因，让人觉得是魔法公式一样。其实它可以从Adaboost的损失函数推导出来。

从另一个角度讲，　Adaboost是模型为加法模型，学习算法为前向分步学习算法，损失函数为指数函数的分类问题。

模型为加法模型好理解，我们的最终的强分类器是若干个弱分类器加权平均而得到的。

前向分步学习算法也好理解，我们的算法是通过一轮轮的弱学习器学习，利用前一个弱学习器的结果来更新后一个弱学习器的训练集权重。也就是说，第k-1轮的强学习器为$$f_{k-1}(x) = sumlimits_{i=1}^{k-1}alpha_iG_{i}(x)$$

而第k轮的强学习器为$$f_{k}(x) = sumlimits_{i=1}^{k}alpha_iG_{i}(x)$$

上两式一比较可以得到$$f_{k}(x) = f_{k-1}(x) + alpha_kG_k(x)$$

可见强学习器的确是通过前向分步学习算法一步步而得到的。

Adaboost损失函数为指数函数，即定义损失函数为$$arg;min;(alpha, G);;sumlimits_{i=1}^{m}exp(-y_if_{k}(x))$$

利用前向分步学习算法的关系可以得到损失函数为$$(alpha_k, G_k(x)) = arg;min;(alpha, G);;sumlimits_{i=1}^{m}exp[(-y_i)(f_{k-1}(x) + alpha G(x))]$$

令$$w_{ki}^{'} = exp(-y_if_{k-1}(x))$$, 它的值不依赖于$$alpha$$, G,因此与最小化无关，仅仅依赖于$$f_{k-1}(x)$$,随着每一轮迭代而改变。

将这个式子带入损失函数,损失函数转化为$$(alpha_k, G_k(x)) = arg;min;(alpha, G);;sumlimits_{i=1}{m}w_{ki}{'}exp[-y_ialpha G(x)]$$

首先，我们求$$G_k(x)$$.，可以得到$$G_k(x) = arg;min;(G);;sumlimits_{i=1}{m}w_{ki}{'}I(y_i neq G(x_i))$$

将$$G_k(x)$$带入损失函数，并对$$alpha$$求导，使其等于0，则就得到了$$alpha_k = frac{1}{2}logfrac{1-e_k}{e_k}$$

其中，$$e_k$$即为我们前面的分类误差率。$$e_k = frac{sumlimits_{i=1}{m}w_{ki}{'}I(y_i neq G(x_i))}{sumlimits_{i=1}{m}w_{ki}{'}} = sumlimits_{i=1}^{m}w_{ki}I(y_i neq G(x_i))$$

最后看样本权重的更新。利用$$f_{k}(x) = f_{k-1}(x) + alpha_kG_k(x)$$和$$w_{ki}{'} = exp(-y_if_{k-1}(x))$$，即可得：
$$w_{k+1,i}{'} = w_{ki}^{'}exp[-y_ialpha_kG_k(x)]$$

这样就得到了我们第二节的样本权重更新公式。

4. AdaBoost二元分类问题算法流程

这里我们对AdaBoost二元分类问题算法流程做一个总结。

输入为样本集$$T={(x_,y_1),(x_2,y_2), ...(x_m,y_m)}$$，输出为{-1, +1}，弱分类器算法, 弱分类器迭代次数K。

输出为最终的强分类器f(x)

1) 初始化样本集权重为$$D(1) = (w_{11}, w_{12}, ...w_{1m}) ;;; w_{1i}=frac{1}{m};;; i =1,2...m$$

2) 对于k=1,2，...K:

a) 使用具有权重$$D_k$$的样本集来训练数据，得到弱分类器$$G_k(x)$$

b)计算$$G_k(x)$$的分类误差率$$e_k = P(G_k(x_i) neq y_i) = sumlimits_{i=1}^{m}w_{ki}I(G_k(x_i) neq y_i)$$

c) 计算弱分类器的系数$$alpha_k = frac{1}{2}logfrac{1-e_k}{e_k}$$

d) 更新样本集的权重分布$$w_{k+1,i} = frac{w_{ki}}{Z_K}exp(-alpha_ky_iG_k(x_i)) ;; i =1,2,...m$$

这里$$Z_k$$是规范化因子$$Z_k = sumlimits_{i=1}^{m}w_{ki}exp(-alpha_ky_iG_k(x_i))$$

3) 构建最终分类器为：$$f(x) = sign(sumlimits_{k=1}^{K}alpha_kG_k(x))$$

对于Adaboost多元分类算法，其实原理和二元分类类似，最主要区别在弱分类器的系数上。比如Adaboost SAMME算法，它的弱分类器的系数$$alpha_k = frac{1}{2}logfrac{1-e_k}{e_k} + log(R-1)$$

其中R为类别数。从上式可以看出，如果是二元分类，R=2，则上式和我们的二元分类算法中的弱分类器的系数一致。

5. Adaboost回归问题的算法流程

这里我们对AdaBoost回归问题算法流程做一个总结。AdaBoost回归算法变种很多，下面的算法为Adaboost R2回归算法过程。

输入为样本集$$T={(x_,y_1),(x_2,y_2), ...(x_m,y_m)}$$，，弱学习器算法, 弱学习器迭代次数K。

输出为最终的强学习器f(x)

1) 初始化样本集权重为$$D(1) = (w_{11}, w_{12}, ...w_{1m}) ;;; w_{1i}=frac{1}{m};;; i =1,2...m$$

2) 对于k=1,2，...K:

a) 使用具有权重$$D_k$$的样本集来训练数据，得到弱学习器$$G_k(x)$$

b) 计算训练集上的最大误差$$E_k= max|y_i - G_k(x_i)|;i=1,2...m$$

c) 计算每个样本的相对误差:

如果是线性误差，则$$e_{ki}= frac{|y_i - G_k(x_i)|}{E_k}$$；

如果是平方误差，则$$e_{ki}= frac{(y_i - G_k(x_i))2}{E_k2}$$

如果是指数误差，则$$e_{ki}= 1 - exp(frac{-y_i + G_k(x_i))}{E_k})$$

d) 计算回归误差率$$e_k = sumlimits_{i=1}^{m}w_{ki}e_{ki}$$

c) 计算弱学习器的系数$$alpha_k =frac{e_k}{1-e_k}$$

d) 更新样本集的权重分布为$$w_{k+1,i} = frac{w_{ki}}{Z_k}alpha_k^{1-e_{ki}}$$

这里$$Z_k$$是规范化因子$$Z_k = sumlimits_{i=1}{m}w_{ki}alpha_k{1-e_{ki}}$$

3) 构建最终强学习器为：$$f(x) = sumlimits_{k=1}^{K}(lnfrac{1}{alpha_k})G_k(x)$$

6. Adaboost算法的正则化

为了防止Adaboost过拟合，我们通常也会加入正则化项，这个正则化项我们通常称为步长(learning rate)。定义为$$nu$$,对于前面的弱学习器的迭代$$f_{k}(x) = f_{k-1}(x) + alpha_kG_k(x)$$

如果我们加上了正则化项，则有$$f_{k}(x) = f_{k-1}(x) + nualpha_kG_k(x)$$

$$nu$$的取值范围为$$0 < nu leq 1$$。对于同样的训练集学习效果，较小的$$nu$$意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。

7. Adaboost小结

到这里Adaboost就写完了，前面有一个没有提到，就是弱学习器的类型。理论上任何学习器都可以用于Adaboost.但一般来说，使用最广泛的Adaboost弱学习器是决策树和神经网络。对于决策树，Adaboost分类用了CART分类树，而Adaboost回归用了CART回归树。

这里对Adaboost算法的优缺点做一个总结。

Adaboost的主要优点有：

1）Adaboost作为分类器时，分类精度很高

2）在Adaboost的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活。

3）作为简单的二元分类器时，构造简单，结果可理解。

4）不容易发生过拟合

Adaboost的主要缺点有：

1）对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性。