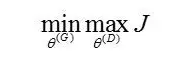当前位置：首页 > 文档资料 > 机器学习原理 >

对抗生成网络(Generative Adversarial Networks)

优质

小牛编辑

129浏览

2023-12-01

本期我们来聊聊GANs（Generativeadversarial networks，对抗式生成网络，也有人译为生成式对抗网络）。GAN最早由Ian Goodfellow于2014年提出，以其优越的性能，在不到两年时间里，迅速成为一大研究热点。

GANs与博弈论

GANs是一类生成模型，从字面意思不难猜到它会涉及两个“对手”，一个称为Generator（生成者），一个称为Discriminator（判别者）。Goodfellow最近arxiv上挂出的GAN tutorial文章中将它们分别比喻为伪造者（Generator）和警察（Discriminator）。伪造者总想着制造出能够以假乱真的钞票，而警察则试图用更先进的技术甄别真假钞票。两者在博弈过程中不断升级自己的技术。

从博弈论的角度来看，如果是零和博弈（zero-sum game），两者最终会达到纳什均衡（Nash equilibrium），即存在一组策略(g, d)，如果Generator不选择策略g，那么对于Discriminator来说，总存在一种策略使得Generator输得更惨；同样地，将Generator换成Discriminator也成立。囚徒的困境就是一个典型的零和博弈。

如果GANs定义的lossfunction满足零和博弈，并且有足够多的样本，双方都有充足的学习能力情况，在这种情况下，Generator和Discriminator的最优策略即为纳什均衡点，也即：Generator产生的都是“真钞”（材料、工艺技术与真钞一样，只是没有得到授权...），Discriminator会把任何一张钞票以1/2的概率判定为真钞。

讲到这里，今天的推送基本就讲完了...

额，至少思想和框架都介绍完了，具体怎么操作呢，大家可以先想一想，然后再往下看。

下面的内容，我们分为三个部分：

为什么要研究生成模型（Generative model）？只是出于好玩吗？
GANs——IanGoodfellow在2014年提出来的版本，以及它的一些演化（GANs有很多种，这里主要介绍最初的版本，其他版本将在以后介绍）
GANs有什么优缺点？

以下内容根据Goodfellow 2014年发表的GAN论文和代码（arxiv 1406.2661）以及近期arxiv上挂出的NIPS tutorial（arxiv 1701.00160 ）整理。

先来讲讲为什么要研究生成模型，首先，生成模型真的很好玩......

还是来看看Ian Goodfellow怎么说吧。

高维概率分布在实际应用中非常常见。训练生成模型，并用生成模型采样可以检验我们对高维概率分布的表示和操纵能力。
生成模型能够嵌入到增强学习（reinforcement learning）的框架中。例如用增强学习求解规划问题，可以用生成模型学习一个条件概率分布，agent可以根据生成模型对不同actions的响应，选择尽可能好的action。
生成模型一般是非监督或者半监督模型，能够处理数据缺失问题，并且还可以用于预测缺失的数据。
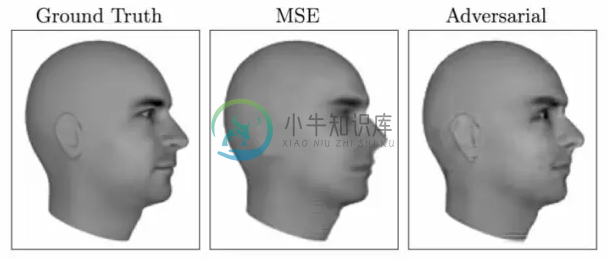
生成模型，特别是GANs，能处理多模态输出（multi-modal）的问题。多模态输出问题（对于离散输出来说，就是多类标问题【multi-label】）是很多机器学习算法没办法直接处理的问题，很多机器学习算法的loss定义为均方误差，它实际上将多种可能的输出做了平均。下图给出了一个预测视频的下一帧的例子，使用MSE训练的结果，图像模糊了（它对所有可能的结果做了平均），而使用GANs训练的结果，则不存在这种问题。

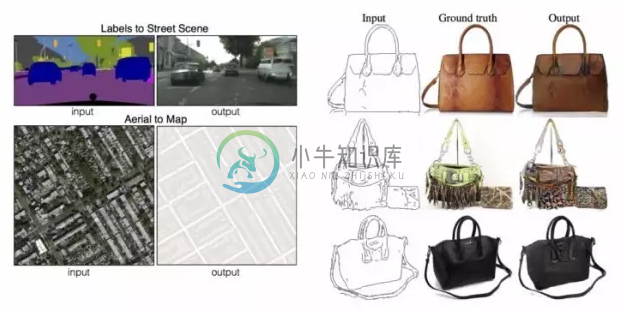
某些任务在本质上要求根据某些分布产生样本。例如：用低分辨率图像产生高分辨率图像；用草图生成真实图像；根据卫星图像产生地图等。如下图所示。

最初版本的GANs模型

GANs在很多应用问题上取得非常好的效果，让生成模型进入人们的视野。前面已经介绍了GANs的思想，接下来，我们就来进一步介绍GANs是怎么做的。

首先，我们需要定义博弈的双方：Generator和Discriminator。

以训练生成图像为例，Generator的任务就是根据输入产生图像。而Discriminator则是判断图像是真实图像还是Generator生成的图像。

Generator和Discriminator具体怎么做可以自己定义。

这里根据我的理解，举个例子：我们知道卷积神经网络能够实现图像抽象特征的提取，如果我们定义Generator的输入为“图像的特征”（训练时没有“图像的特征”，输入可以是随机的噪声向量），那么可以用含有反卷积层或者上采样层的网络实现图像的重构，也就是图像的生成。

Discriminator是一个二元分类器，输入是图像，输出是两类：“自然”图像/Generator产生的图像。这里说的“自然”图像并不一定是自然图像，可以是合成的图像，人眼看上去图像是自然的。二元分类器有很多种，卷积神经网络是一个不错的选择。

其次，要定义loss function才能训练。前面说了，GANs可以看成一个博弈，那么博弈双方都会有cost（代价），如果是零和博弈，那么双方的cost之和为0。Discriminator是一个分类器，它的loss可以定义用交叉熵来定义：

$$J{(D)}(\theta{(D)},\theta^{(G)})=-\frac {1}{2}E_{xP\sim _{data}}logD(x)-\frac {1}{2}E_zlog(1-D(G(z)))$$

如果是零和博弈，那么Generator的loss就定义为：

$$J{(D)}(\theta{(D)},\theta{(G)})=-J{(D)}(\theta{(D)},\theta{(G)})=\frac {1}{2}E_{xP\sim _{data}}logD(x)+\frac {1}{2}E_zlog(1-D(G(z)))$$

整个优化问题就是一个minmax博弈：

Goodfellow在2014年的论文中证明了在理想情况下（博弈双方的学习能够足够强、拥有足够的数据、每次迭代过程中，固定Generator，Discriminator总能达到最优），这样构造的GANs会收敛到纳什均衡解。基于此，在2014年的论文里面，作者提出的算法是，每次迭代过程包括两个步骤：更新k次Discriminator（k>=1）；更新1次Generator。也就是，应该让Discriminator学得更充分一些。PS：2016 NIPS tutorial中，作者指出，每次迭代对博弈双方同时进行（随机）梯度下降，在实际操作中效果最好。

然而，这样定义的零和博弈在实际中效果并不好，实际训练的时候，Discriminator仍然采用前面介绍的loss，但Generator采用下面的loss：

$$J{(D)}(\theta{(D)},\theta^{(G)})=-\frac {1}{2}E_zlog(1-D(G(z)))$$

也就是说，Generator的loss只考虑它自身的交叉熵，而不用全局的交叉熵。这样做能够确保任一博弈失利的一方仍有较强的梯度以扭转不利局面。作者称采用这个loss的博弈为Non-saturating heuristic game。采用这个版本的loss，整个博弈不再是零和博弈，没有理论保证它会收敛达到纳什均衡。

最大似然博弈GANs

原始版本的GANs模型并不是通过最大化似然函数（也即最小化KL散度）来训练的。Goodfellow在14年的另一篇论文（https://arxiv.org/abs/1412.6515）中证明了，若每次迭代Discriminator都达到最优，Generator采用下面的loss，则GANs等价于最大化似然函数：

$$J{(G)}=-\frac{1}{2}E_zexp(\sigma {-1}(D(G(z))))$$

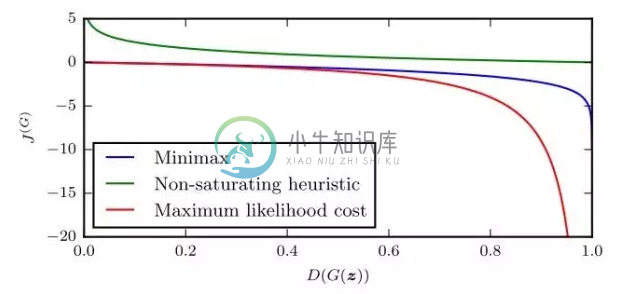
至此，本文总共出现了三种loss，它们的函数图像长这样：

**
**

GANs实验效果

根据Goodfellow 2014年的论文，GANs在MNIST和TFD数据集上训练，产生的样本更接近于真实分布（参看下图中的Table 1）。然而，虽然效果更好，GANs也存在一些问题（如下面的Figure 29和30），话不多说，看图。

GANs优缺点

优点：

相比于FVBNs（全可见信念网络，Fully visible belief networks）模型，GANs能并行生成样本，不需要逐维产生。
相比于玻尔兹曼机（Boltzmann machines）、非线性ICA（non-linear ICA）等生成模型，GANs对Generator的设计的限制很少。
理论上保证了某些GANs能够收敛到纳什均衡。
最重要的是，相比于其他生成模型，GANs产生的样本更好。（这一条是主观判断...）

缺点：

训练GANs实际上是在找纳什均衡解，这比优化一个目标函数要困难。
GANs生成的图像比较sharp，也就是说，它倾向于生成相似的图像。作者在2016 NIPS tutorial中指出，这个缺陷与采用何种KL散度作为loss无关，而可能是与训练过程有关。详细的讨论可以参看参考文献2的3.2.5和5.1.1章节。PS：这是一个非常重要的问题，如果想深入理解GANs，请务必阅读原文详细了解。

PS：如果看完你还是没理解是怎么做的，那就看代码吧，网上的代码很多，点击阅读原文（Ian Goodfellow 2014年论文的代码）或者看文末给的代码链接（有simple版本的代码）。阅读源码对于理解文献的方法有很大的好处（前提是源码好理解...）；看完论文自己复现论文结果对于进一步理解论文，甚至改进方法都有很大的帮助。这也是我目前在做的事情。

参考文献

Goodfellow I,Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]//Advances inNeural Information Processing Systems. 2014: 2672-2680.
Goodfellow I.NIPS 2016 Tutorial: Generative Adversarial Networks[J]. arXiv preprintarXiv:1701.00160, 2016.
Goodfellow IJ. On distinguishability criteria for estimating generative models[J]. arXivpreprint arXiv:1412.6515, 2014.

GANs代码

Theano+pylearn2版本（Goodfellow提供）： https://github.com/goodfeli/adversarial
Keras版本： https://github.com/jhayes14/GAN
Tensorflow版本（含GANs+VAEs+DRAW）： https://github.com/ikostrikov/TensorFlow-VAE-GAN-DRAW

各种GAN

The GAN Zoo

Every week, new GAN papers are coming out and it's hard to keep track of them all, not to mention the incredibly creative ways in which researchers are naming these GANs! So, here's a list of what started as a fun activity compiling all named GANs!

You can also check out the same data in a tabular format with functionality to filter by year or do a quick search by title here.

Contributions are welcome. Add links through pull requests or create an issue to lemme know something I missed or to start a discussion.

Check out Deep Hunt - my weekly AI newsletter for this repo as blogpost and follow me on Twitter.

3D-GAN - Learning a Probabilistic Latent Space of Object Shapes via 3D Generative-Adversarial Modeling (github)
3D-IWGAN - Improved Adversarial Systems for 3D Object Generation and Reconstruction (github)
3D-RecGAN - 3D Object Reconstruction from a Single Depth View with Adversarial Learning (github)
ABC-GAN - ABC-GAN: Adaptive Blur and Control for improved training stability of Generative Adversarial Networks (github)
AC-GAN - Conditional Image Synthesis With Auxiliary Classifier GANs
acGAN - Face Aging With Conditional Generative Adversarial Networks
AdaGAN - AdaGAN: Boosting Generative Models
AE-GAN - AE-GAN: adversarial eliminating with GAN
AEGAN - Learning Inverse Mapping by Autoencoder based Generative Adversarial Nets
AffGAN - Amortised MAP Inference for Image Super-resolution
AL-CGAN - Learning to Generate Images of Outdoor Scenes from Attributes and Semantic Layouts
ALI - Adversarially Learned Inference
AlignGAN - AlignGAN: Learning to Align Cross-Domain Images with Conditional Generative Adversarial Networks
AM-GAN - Activation Maximization Generative Adversarial Nets
AnoGAN - Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery
ARAE - Adversarially Regularized Autoencoders for Generating Discrete Structures (github)
ARDA - Adversarial Representation Learning for Domain Adaptation
ARIGAN - ARIGAN: Synthetic Arabidopsis Plants using Generative Adversarial Network
ArtGAN - ArtGAN: Artwork Synthesis with Conditional Categorial GANs
b-GAN - Generative Adversarial Nets from a Density Ratio Estimation Perspective
Bayesian GAN - Deep and Hierarchical Implicit Models
Bayesian GAN - Bayesian GAN
BCGAN - Bayesian Conditional Generative Adverserial Networks
BEGAN - BEGAN: Boundary Equilibrium Generative Adversarial Networks
BGAN - Binary Generative Adversarial Networks for Image Retrieval (github)
BiGAN - Adversarial Feature Learning
BS-GAN - Boundary-Seeking Generative Adversarial Networks
C-RNN-GAN - C-RNN-GAN: Continuous recurrent neural networks with adversarial training (github)
CaloGAN - CaloGAN: Simulating 3D High Energy Particle Showers in Multi-Layer Electromagnetic Calorimeters with Generative Adversarial Networks (github)
CAN - CAN: Creative Adversarial Networks, Generating Art by Learning About Styles and Deviating from Style Norms
CatGAN - Unsupervised and Semi-supervised Learning with Categorical Generative Adversarial Networks
CausalGAN - CausalGAN: Learning Causal Implicit Generative Models with Adversarial Training
CC-GAN - Semi-Supervised Learning with Context-Conditional Generative Adversarial Networks (github)
CDcGAN - Simultaneously Color-Depth Super-Resolution with Conditional Generative Adversarial Network
CGAN - Conditional Generative Adversarial Nets
CGAN - Controllable Generative Adversarial Network
Chekhov GAN - An Online Learning Approach to Generative Adversarial Networks
CoGAN - Coupled Generative Adversarial Networks
Conditional cycleGAN - Conditional CycleGAN for Attribute Guided Face Image Generation
constrast-GAN - Generative Semantic Manipulation with Contrasting GAN
Context-RNN-GAN - Contextual RNN-GANs for Abstract Reasoning Diagram Generation
Coulomb GAN - Coulomb GANs: Provably Optimal Nash Equilibria via Potential Fields
Cramèr GAN - The Cramer Distance as a Solution to Biased Wasserstein Gradients
crVAE-GAN - Channel-Recurrent Variational Autoencoders
CS-GAN - Improving Neural Machine Translation with Conditional Sequence Generative Adversarial Nets
CVAE-GAN - CVAE-GAN: Fine-Grained Image Generation through Asymmetric Training
CycleGAN - Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks (github)
D2GAN - Dual Discriminator Generative Adversarial Nets
DAN - Distributional Adversarial Networks
DCGAN - Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks (github)
DeliGAN - DeLiGAN : Generative Adversarial Networks for Diverse and Limited Data (github)
DiscoGAN - Learning to Discover Cross-Domain Relations with Generative Adversarial Networks
DistanceGAN - One-Sided Unsupervised Domain Mapping
DM-GAN - Dual Motion GAN for Future-Flow Embedded Video Prediction
DR-GAN - Representation Learning by Rotating Your Faces
DRAGAN - How to Train Your DRAGAN (github)
DSP-GAN - Depth Structure Preserving Scene Image Generation
DTN - Unsupervised Cross-Domain Image Generation
DualGAN - DualGAN: Unsupervised Dual Learning for Image-to-Image Translation
Dualing GAN - Dualing GANs
EBGAN - Energy-based Generative Adversarial Network
ED//GAN - Stabilizing Training of Generative Adversarial Networks through Regularization
EGAN - Enhanced Experience Replay Generation for Efficient Reinforcement Learning
ExprGAN - ExprGAN: Facial Expression Editing with Controllable Expression Intensity
f-GAN - f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization
FF-GAN - Towards Large-Pose Face Frontalization in the Wild
Fila-GAN - Synthesizing Filamentary Structured Images with GANs
Fisher GAN - Fisher GAN
Flow-GAN - Flow-GAN: Bridging implicit and prescribed learning in generative models
GAMN - Generative Adversarial Mapping Networks
GAN - Generative Adversarial Networks (github)
GAN-CLS - Generative Adversarial Text to Image Synthesis (github)
GAN-sep - GANs for Biological Image Synthesis (github)
GAN-VFS - Generative Adversarial Network-based Synthesis of Visible Faces from Polarimetric Thermal Faces
GANCS - Deep Generative Adversarial Networks for Compressed Sensing Automates MRI
GAWWN - Learning What and Where to Draw (github)
GeneGAN - GeneGAN: Learning Object Transfiguration and Attribute Subspace from Unpaired Data (github)
Geometric GAN - Geometric GAN
GMAN - Generative Multi-Adversarial Networks
GMM-GAN - Towards Understanding the Dynamics of Generative Adversarial Networks
GoGAN - Gang of GANs: Generative Adversarial Networks with Maximum Margin Ranking
GP-GAN - GP-GAN: Towards Realistic High-Resolution Image Blending (github)
GRAN - Generating images with recurrent adversarial networks (github)
IAN - Neural Photo Editing with Introspective Adversarial Networks (github)
IcGAN - Invertible Conditional GANs for image editing (github)
ID-CGAN - Image De-raining Using a Conditional Generative Adversarial Network
iGAN - Generative Visual Manipulation on the Natural Image Manifold (github)
Improved GAN - Improved Techniques for Training GANs (github)
InfoGAN - InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets (github)
IRGAN - IRGAN: A Minimax Game for Unifying Generative and Discriminative Information Retrieval models
IWGAN - On Unifying Deep Generative Models
l-GAN - Representation Learning and Adversarial Generation of 3D Point Clouds
LAGAN - Learning Particle Physics by Example: Location-Aware Generative Adversarial Networks for Physics Synthesis
LAPGAN - Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks (github)
LD-GAN - Linear Discriminant Generative Adversarial Networks
LDAN - Label Denoising Adversarial Network (LDAN) for Inverse Lighting of Face Images
LeakGAN - Long Text Generation via Adversarial Training with Leaked Information
LeGAN - Likelihood Estimation for Generative Adversarial Networks
LR-GAN - LR-GAN: Layered Recursive Generative Adversarial Networks for Image Generation
LS-GAN - Loss-Sensitive Generative Adversarial Networks on Lipschitz Densities
LSGAN - Least Squares Generative Adversarial Networks
MAD-GAN - Multi-Agent Diverse Generative Adversarial Networks
MAGAN - MAGAN: Margin Adaptation for Generative Adversarial Networks
MalGAN - Generating Adversarial Malware Examples for Black-Box Attacks Based on GAN
MaliGAN - Maximum-Likelihood Augmented Discrete Generative Adversarial Networks
MARTA-GAN - Deep Unsupervised Representation Learning for Remote Sensing Images
McGAN - McGan: Mean and Covariance Feature Matching GAN
MD-GAN - Learning to Generate Time-Lapse Videos Using Multi-Stage Dynamic Generative Adversarial Networks
MDGAN - Mode Regularized Generative Adversarial Networks
MedGAN - Generating Multi-label Discrete Electronic Health Records using Generative Adversarial Networks
MGAN - Precomputed Real-Time Texture Synthesis with Markovian Generative Adversarial Networks (github)
MGGAN - Multi-Generator Generative Adversarial Nets
MIX+GAN - Generalization and Equilibrium in Generative Adversarial Nets (GANs)
MMD-GAN - MMD GAN: Towards Deeper Understanding of Moment Matching Network (github)
MMGAN - MMGAN: Manifold Matching Generative Adversarial Network for Generating Images
MoCoGAN - MoCoGAN: Decomposing Motion and Content for Video Generation (github)
MPM-GAN - Message Passing Multi-Agent GANs
MuseGAN - MuseGAN: Symbolic-domain Music Generation and Accompaniment with Multi-track Sequential Generative Adversarial Networks
MV-BiGAN - Multi-view Generative Adversarial Networks
OptionGAN - OptionGAN: Learning Joint Reward-Policy Options using Generative Adversarial Inverse Reinforcement Learning
ORGAN - Objective-Reinforced Generative Adversarial Networks (ORGAN) for Sequence Generation Models
PAN - Perceptual Adversarial Networks for Image-to-Image Transformation
PassGAN - PassGAN: A Deep Learning Approach for Password Guessing
Perceptual GAN - Perceptual Generative Adversarial Networks for Small Object Detection
PGAN - Probabilistic Generative Adversarial Networks
pix2pix - Image-to-Image Translation with Conditional Adversarial Networks (github)
PixelGAN - PixelGAN Autoencoders
Pose-GAN - The Pose Knows: Video Forecasting by Generating Pose Futures
PPGN - Plug & Play Generative Networks: Conditional Iterative Generation of Images in Latent Space
PrGAN - 3D Shape Induction from 2D Views of Multiple Objects
PSGAN - Learning Texture Manifolds with the Periodic Spatial GAN
RankGAN - Adversarial Ranking for Language Generation
RCGAN - Real-valued (Medical) Time Series Generation with Recurrent Conditional GANs
RefineGAN - Compressed Sensing MRI Reconstruction with Cyclic Loss in Generative Adversarial Networks
RenderGAN - RenderGAN: Generating Realistic Labeled Data
ResGAN - Generative Adversarial Network based on Resnet for Conditional Image Restoration
RNN-WGAN - Language Generation with Recurrent Generative Adversarial Networks without Pre-training (github)
RPGAN - Stabilizing GAN Training with Multiple Random Projections (github)
RTT-GAN - Recurrent Topic-Transition GAN for Visual Paragraph Generation
RWGAN - Relaxed Wasserstein with Applications to GANs
SAD-GAN - SAD-GAN: Synthetic Autonomous Driving using Generative Adversarial Networks
SalGAN - SalGAN: Visual Saliency Prediction with Generative Adversarial Networks (github)
SBADA-GAN - From source to target and back: symmetric bi-directional adaptive GAN
SD-GAN - Semantically Decomposing the Latent Spaces of Generative Adversarial Networks
SEGAN - SEGAN: Speech Enhancement Generative Adversarial Network
SeGAN - SeGAN: Segmenting and Generating the Invisible
SegAN - SegAN: Adversarial Network with Multi-scale L1 Loss for Medical Image Segmentation
SeqGAN - SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient (github)
SGAN - Texture Synthesis with Spatial Generative Adversarial Networks
SGAN - Stacked Generative Adversarial Networks (github)
SGAN - Steganographic Generative Adversarial Networks
SimGAN - Learning from Simulated and Unsupervised Images through Adversarial Training
SketchGAN - Adversarial Training For Sketch Retrieval
SL-GAN - Semi-Latent GAN: Learning to generate and modify facial images from attributes
SN-GAN - Spectral Normalization for Generative Adversarial Networks (github)
Softmax-GAN - Softmax GAN
Splitting GAN - Class-Splitting Generative Adversarial Networks
SRGAN - Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network
SS-GAN - Semi-supervised Conditional GANs
ss-InfoGAN - Guiding InfoGAN with Semi-Supervision
SSGAN - SSGAN: Secure Steganography Based on Generative Adversarial Networks
SSL-GAN - Semi-Supervised Learning with Context-Conditional Generative Adversarial Networks
ST-GAN - Style Transfer Generative Adversarial Networks: Learning to Play Chess Differently
StackGAN - StackGAN: Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks
SteinGAN - Learning Deep Energy Models: Contrastive Divergence vs. Amortized MLE
S^2GAN - Generative Image Modeling using Style and Structure Adversarial Networks
TAC-GAN - TAC-GAN - Text Conditioned Auxiliary Classifier Generative Adversarial Network (github)
TAN - Outline Colorization through Tandem Adversarial Networks
TextureGAN - TextureGAN: Controlling Deep Image Synthesis with Texture Patches
TGAN - Temporal Generative Adversarial Nets
TP-GAN - Beyond Face Rotation: Global and Local Perception GAN for Photorealistic and Identity Preserving Frontal View Synthesis
Triple-GAN - Triple Generative Adversarial Nets
Unrolled GAN - Unrolled Generative Adversarial Networks (github)
VAE-GAN - Autoencoding beyond pixels using a learned similarity metric
VariGAN - Multi-View Image Generation from a Single-View
VAW-GAN - Voice Conversion from Unaligned Corpora using Variational Autoencoding Wasserstein Generative Adversarial Networks
VEEGAN - VEEGAN: Reducing Mode Collapse in GANs using Implicit Variational Learning (github)
VGAN - Generating Videos with Scene Dynamics (github)
VGAN - Generative Adversarial Networks as Variational Training of Energy Based Models (github)
ViGAN - Image Generation and Editing with Variational Info Generative Adversarial Networks
VIGAN - VIGAN: Missing View Imputation with Generative Adversarial Networks
VRAL - Variance Regularizing Adversarial Learning
WaterGAN - WaterGAN: Unsupervised Generative Network to Enable Real-time Color Correction of Monocular Underwater Images
WGAN - Wasserstein GAN (github)
WGAN-GP - Improved Training of Wasserstein GANs (github)
WS-GAN - Weakly Supervised Generative Adversarial Networks for 3D Reconstruction
α-GAN - Variational Approaches for Auto-Encoding Generative Adversarial Networks (github)
Δ-GAN - Triangle Generative Adversarial Networks

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。