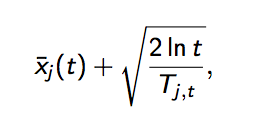假设每个臂是否产生收益，其背后有一个概率分布，产生收益的概率为p

我们不断地试验，去估计出一个置信度较高的*概率p的概率分布*就能近似解决这个问题了。

怎么能估计概率p的概率分布呢？ 答案是假设概率p的概率分布符合beta(wins, lose)分布，它有两个参数: wins, lose。

每个臂都维护一个beta分布的参数。每次试验后，选中一个臂，摇一下，有收益则该臂的wins增加1，否则该臂的lose增加1。

每次选择臂的方式是：用每个臂现有的beta分布产生一个随机数b，选择所有臂产生的随机数中最大的那个臂去摇。

以上就是Thompson采样，用python实现就一行：

choice = numpy.argmax(pymc.rbeta(1 + self.wins, 1 + self.trials - self.wins))

Upper Confidence Bound(置信区间上界)

先对每一个臂都试一遍

之后，每次选择以下值最大的那个臂

其中加号前面是这个臂到目前的收益均值，后面的叫做bonus，本质上是均值的标准差，t是目前的试验次数，Tjt是这个臂被试次数。

这个公式反映：均值越大，标准差越小，被选中的概率会越来越大，起到了exploit的作用；同时哪些被选次数较少的臂也会得到试验机会，起到了explore的作用。

Epsilon-Greedy算法

选一个(0,1)之间较小的数epsilon

每次以概率epsilon（产生一个[0,1]之间的随机数，比epsilon小）做一件事：所有臂中随机选一个。否则，选择截止当前，平均收益最大的那个臂。

是不是简单粗暴？epsilon的值可以控制对Exploit和Explore的偏好程度。越接近0，越保守，只想花钱不想挣钱。