5.算法原理以及算法效果（哨岗相机）

定位原理

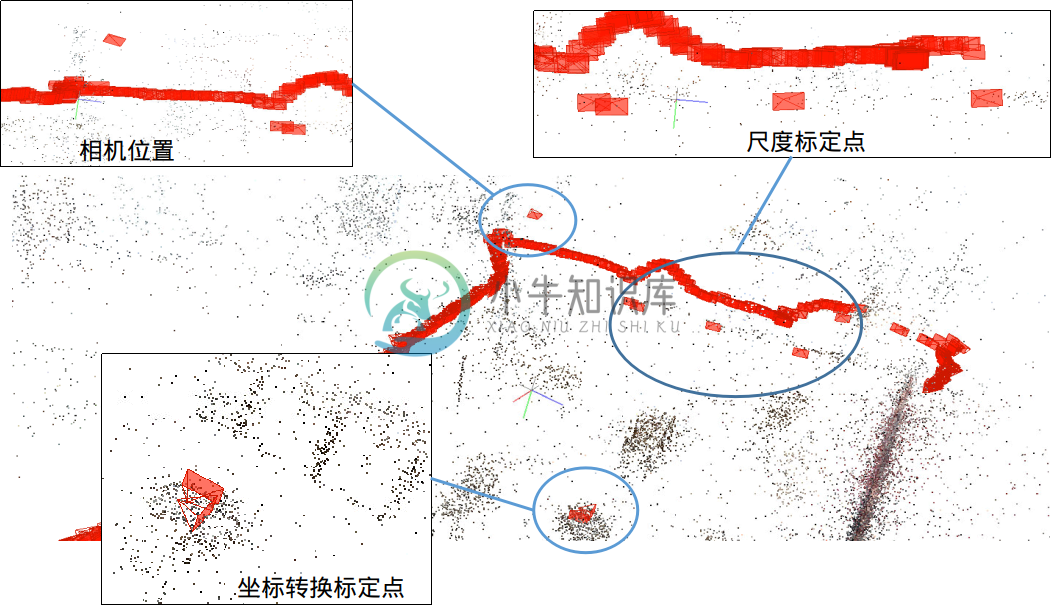
基本原理是 sfm(Structure From Motion)， 通过一系列运动图像，求得相机位姿，然后加入带有尺度信息的一组图片（拍摄的位置已知），然后进行三维重建，最后得到放置哨岗相机处成像平面相对地图原点位姿，然后检测到的机器人像素坐标通过内参矩阵与地面平面方程联立方程组，解得地面平面坐标。

相机位姿求解

整个模块的任务是获取固定在高空2m左右的哨岗相机相对于地图中心坐标点所在坐标系的变换矩阵。我们基于增量式sfm算法，对每张图片检测特征点，再对每对图片中的特征点进行匹配，只保留满足几何约束的匹配，最后执行一个迭代式的、鲁棒的SfM方法来估计摄像机的内参和外参，由于内参已经事先进行标定，因此只需要获取结果中的外参，即相机到世界的坐标变换矩阵。

​

图 5.1 三维重建效果图

图 5.2 哨岗相机视角以及特征点

图 5.3 哨岗相机与其他相机位置共视

利用colmap，可以完成三维重建，利用高精度的三维重建效果获得相机位置以及姿态，将相机放置在已知位置，可以获得尺度信息，消除建图的尺度不确定性，并且可以获得建图坐标系与场地世界坐标转换关系。

图 5.4 特殊标定位置

机器人坐标求解

由之前的检测算法我们可以得到在相机图片里，框出目标机器人位置的方框，以及机器人所在图片中位置的二维点坐标，我们将此坐标定义为像素坐标系下的坐标，并且用表示。

我们将展示基于程序运行过程中具体某一帧的实例来形象地解释相机检测过程中对机器人坐标求解问题。如下图所示，我们从目标检测模块或者目标跟踪获得了目标机器人在二维图像中的坐标点，我们取图中红色方框圈出的红色二号机器人为例。设该方框中心的图像坐标为,已知该相机的内参矩阵为

那么我们根据像素坐标系到相机坐标系的转换关系可以求得机器人在相机坐标系下的坐标点,记为,其中由于目标位置到相机光心的深度未知，是未知的，但是我们可以将该坐标点归一化到的平面上，则此时相机的坐标点可以表示为,其中包含以下关系：

再由像素-相机坐标系转换关系，即：

求得相机坐标系下的坐标

​

图 5.5 机器人像素坐标

根据上述公式，现在我们已经得到了哨岗相机相机坐标系下的目标点空间位置坐标，由于默认的相机坐标系是轴垂直相机光心向前的，初次之外，该坐标系的轴与轴与我们规定的相机自身的坐标系也稍有区别,如下图所示。图中相机坐标系的轴是垂直光心向前的，三个坐标轴分别为轴－红色，轴－绿色，轴－蓝色。

​ ​​

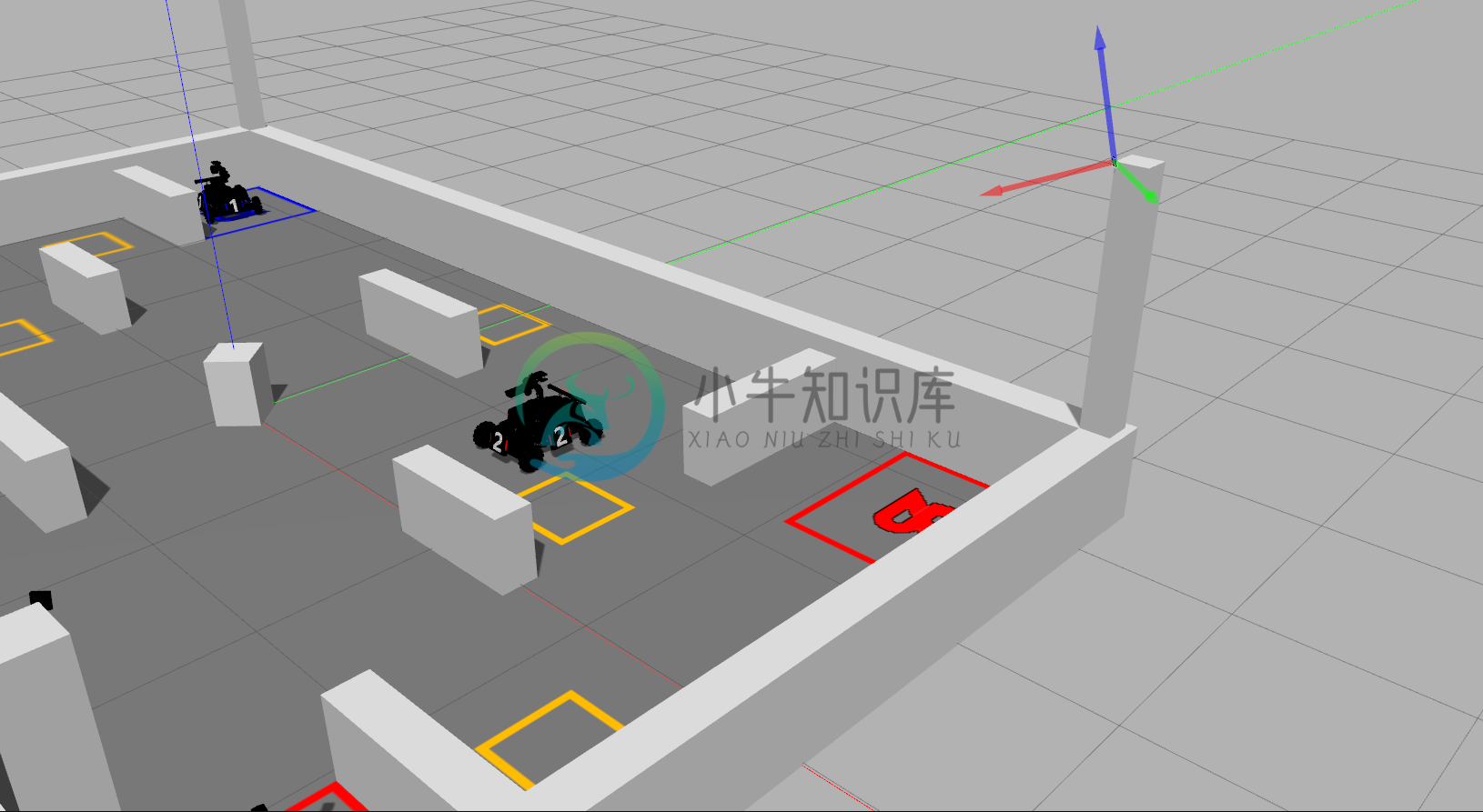
图 5.6 相机坐标系

设后者（我们所规定的）坐标系内的坐标点为,转换的关系即：

之后，我们由相机位姿求解模块获得的结果，即从世界坐标系（如下图所示）到我们规定的相机坐标系的转换关系，可以求得之前归一化平面上的点在世界坐标系的坐标，我们连接该点到相机的光心，得到一条射线，现在求该射线与世界坐标系下机器人所在平面，近似为的交点，即可获得机器人在世界坐标系下的坐标点。

我们设相机位姿求解的结果为,世界坐标系下的点设为，他们分别表示从相机坐标系到世界坐标系坐标转换的旋转矩阵和平移矩阵，则有相机－世界坐标转换关系，注意，这里的相机坐标系下的坐标点实际上是转换到我们规定的相机坐标系下的点。

最终我们得到机器人在世界坐标系下的坐标点,轴的坐标取决于机器人所在平面的高度，这里是取的情况。在实际的测试中，最终获得的目标点与实际点的坐标误差在10-20cm左右。以下动态图展示了哨岗相机的目标定位在仿真环境中的测试效果。
（闪烁效果因为我们检测主要在实物训练集上进行，对于仿真环境，容易出现漏检测情况）

图 5.7 哨岗相机对四辆车进行在地图中的定位

由于在仿真环境中，红蓝机器人在哨岗相机视角中很难分辨，因此我们在仿真环境中没有识别红蓝机器人，并且通过机器人自身的定位，结合哨岗提供的所有机器人位置，完全可以分辨敌我机器人。