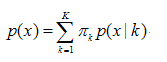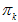混合高斯模型
优质
小牛编辑
197浏览
2023-12-01
1)概述
正太分布也叫高斯分布,正太分布的概率密度曲线也叫高斯分布概率曲线_。_
GaussianMixtureModel(混合高斯模型,GMM)。
聚类算法大多数通过相似度来判断,而相似度又大多采用欧式距离长短作为衡量依据。而GMM采用了新的判断依据:概率,即通过属于某一类的概率大小来判断最终的归属类别。
GMM的基本思想就是:任意形状的概率分布都可以用多个高斯分布函数去近似,也就是说GMM就是有多个单高斯密度分布(Gaussian)组成的,每个Gaussian叫一个"Component",这些"Component"线性加成在一起就组成了 GMM 的概率密度函数,也就是下面的函数。
2)数学公式
K:模型的个数,即Component的个数(聚类的个数)
p(x |k) 则为第k个高斯概率密度,其均值为μk,方差为σk
上述参数,除了K是直接给定之外,其他参数都是通过EM算法估算出来的。(有个参数是指定EM算法参数的)
3)GaussianMixtureModel 算法函数
a)from sklearn.mixture.GaussianMixture
b)主要参数(详细参数)
n_components :高斯模型的个数,即聚类的目标个数
covariance_type : 通过EM算法估算参数时使用的协方差类型,默认是"full"
full:每个模型使用自己的一般协方差矩阵
tied:所用模型共享一个一般协方差矩阵
diag:每个模型使用自己的对角线协方差矩阵
spherical:每个模型使用自己的单一方差